All About Cartpole
Cartpole is one of the very ancient and classical RL-for-control benchmark, early appeared in [Barto et al. 1983]. Many RL algorithms from value-based to policy-based, model-free to model-based were justified under it or its variants encompassing simulations and real robots, i.e.[PILCO].
This post is trying to cover the insights derived from the performances of classical RL algorithms under Cartpole environment. The algorithm descriptions are at Basic Reinforcement Learning, Temporal-Difference Learning, Policy Gradient and Actor-Critic. Ipython notebooks are available at [Cartpole Q, SARSA], [Cartpole REINFORCE]
(Temporary) Related algorithms:
- Q-learning (box, bins): discrete states, discrete actions
- SARSA(λ): linear function approximator for continuous states, discrete actions
- DQN: non-linear function approximator for continuous states, discrete actions
- REINFORCE and baseline: linear Gaussian policy for continuous actions, continuous states
- and more
Temporary Results with 10 runs in CartPole-v0:
Q: [162]-Box, RBF: [6,6,9,9], DQN: 3x[200 hidden]-MLP
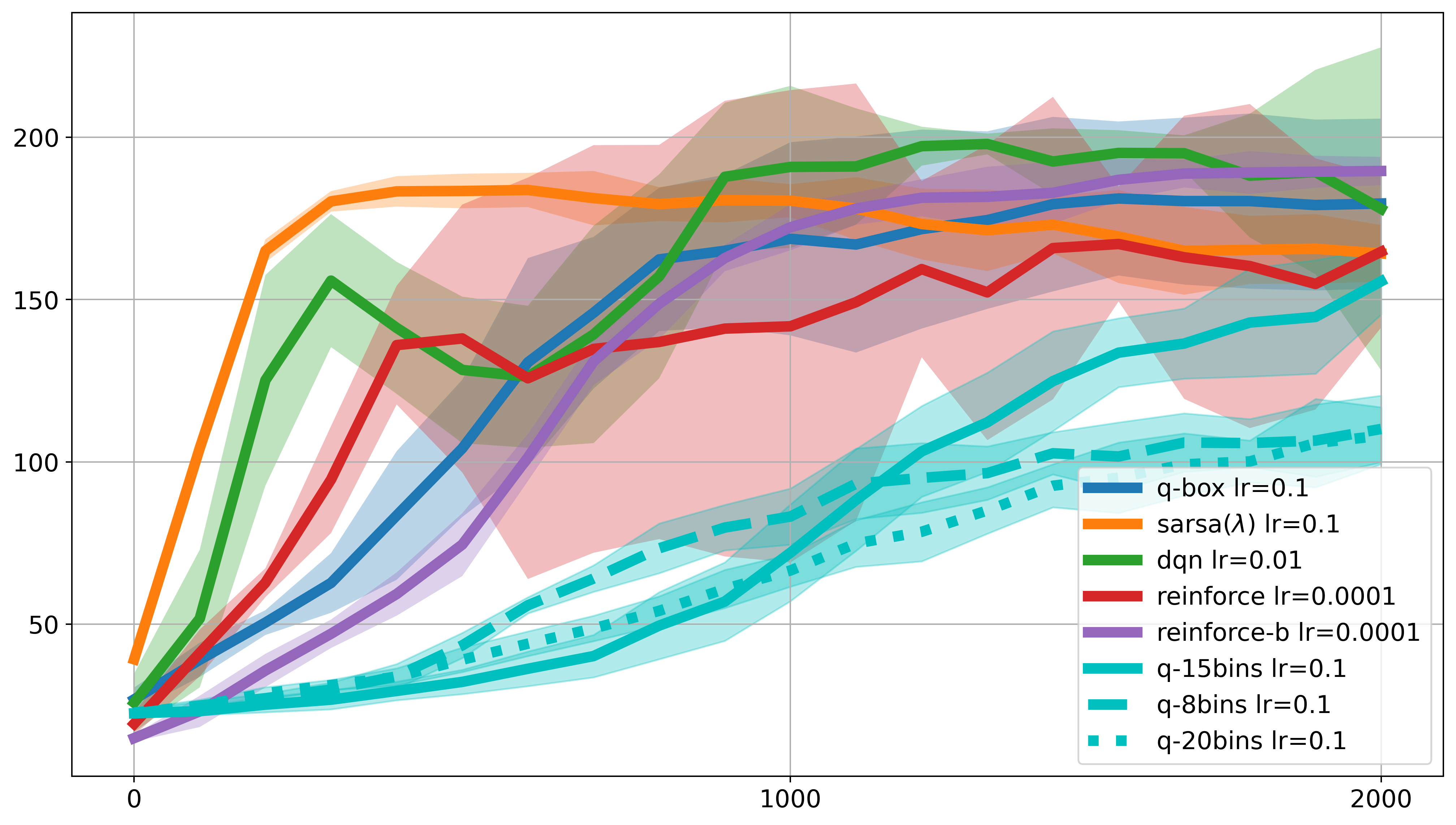
Temporary Summary:
-
SARSA(\(\lambda\)) achieved the best sample efficiency; DQN could reach relatively higher returns; REINFORCE has variance issue, while this can be relieved by adding a baseline
-
Q-learning with box discretization and binning requires more episodes (3000 or more) to converge, since its Q-value hasn’t reached 100 like RBF and DQN
-
a proper number of equal-distance binning of the states will be 15, but the overall performance of binning is worst than box discretization. This suggests that we have to carefully design and divide the states in discrete state cases
-
from the heatmap of the learned value in x=0 and x_dot=0, the highest optimal values learned by RBF and DQN are on diagonal sides from the center. This might be the cause of binary discrete actions (check continous action case for future work)
-
finer RBF networks may not approximate value funtion well but can achieve better sample efficiency
-
DQN requires smaller learning rate for stable learning, say 0.01 or 0.001 compared to Q-box and SARSA(\(\lambda\))s’ 0.1
-
3-layer network can capture quite nice value approximation compared to 2-layer or 1-layer wider network
-
discounting factor remains 0.99 is good
Future work:
-
analyze and visualize weights and gradients of DQN and RBF
-
tune NN capacities, check different activation functions, e.g. SiLU or try NRBF
-
increase the difficulty of the task by setting threshold to 180deg or to longer step length
-
test different reward functions
-
test different algs with continuous controllers
Problem Setup
[OpenAI CartPole-v0], ends in 200 episodes
[OpenAI CartPole-v1], ends in 500 episodes
[Env source code-v1]
[Env Continuous actions]
| Num | Observation | Min | Max |
|---|---|---|---|
| 0 | Cart Position | -4.8 | 4.8 |
| 1 | Cart Velocity | -Inf | Inf |
| 2 | Pole Angle | ~ -0.418 rad (-24°) | ~ 0.418 rad (24°) |
| 3 | Pole Angular Velocity | -Inf | Inf |
| Num | Action |
|---|---|
| 0 | Push cart to the left with 10N |
| 1 | Push cart to the right with 10N |
State variables: (4,)
- \(x\) - cart position
- \(\dot{x}\) - cart velocity
- \(\theta\) - pole angle
- \(\dot{\theta}\) - pole angular velocity
Action variables: (2,)
Reward: +1 unless termination
Termination:
- \(\theta < -15^o\) or \(\theta > 15^o\), 15 degree = 0.2618 rad
- \(x<-2.4\) or \(x>2.4\)
Q-box
Box System [Michie et al. 1968] divided the state variables into 3x3x6x3 boxes as follows:
| variable | range | |||||
|---|---|---|---|---|---|---|
| \(x\) | <-0.8 | (-0.8,0.8) | >0.8 | |||
| box: | +0 | +1 | +2 | |||
| \(\dot{x}\) | <-0.5 | (-0.5,0.5 | >0.5 | |||
| box: | +0 | +3 | +6 | |||
| \(\theta\)(deg) | <-12 | (-12,-1.5) | (-1.5,0) | (0,1.5) | (1.5,12) | >12 |
| box: | +0 | +9 | +18 | +27 | +36 | +45 |
| \(\dot{\theta}\) | <-50 | (-50,50) | >50 | |||
| box: | +0 | +54 | +108 |
Experimental setting:
- State space: (4,) continuous -> (162,)
- Action sapce: (2,)
- episode length: 2000
- step length: 200 in CartPole-v0
- learning rate (lr): 0.1
- discounting factor (gm): 0.99
- exploration factor (epsilon): from 1, epsilon*=epsilon_decay_rate for each episode
- exploration decaying rate (epsilon decay rate): 0.995
Learned optimal Values:
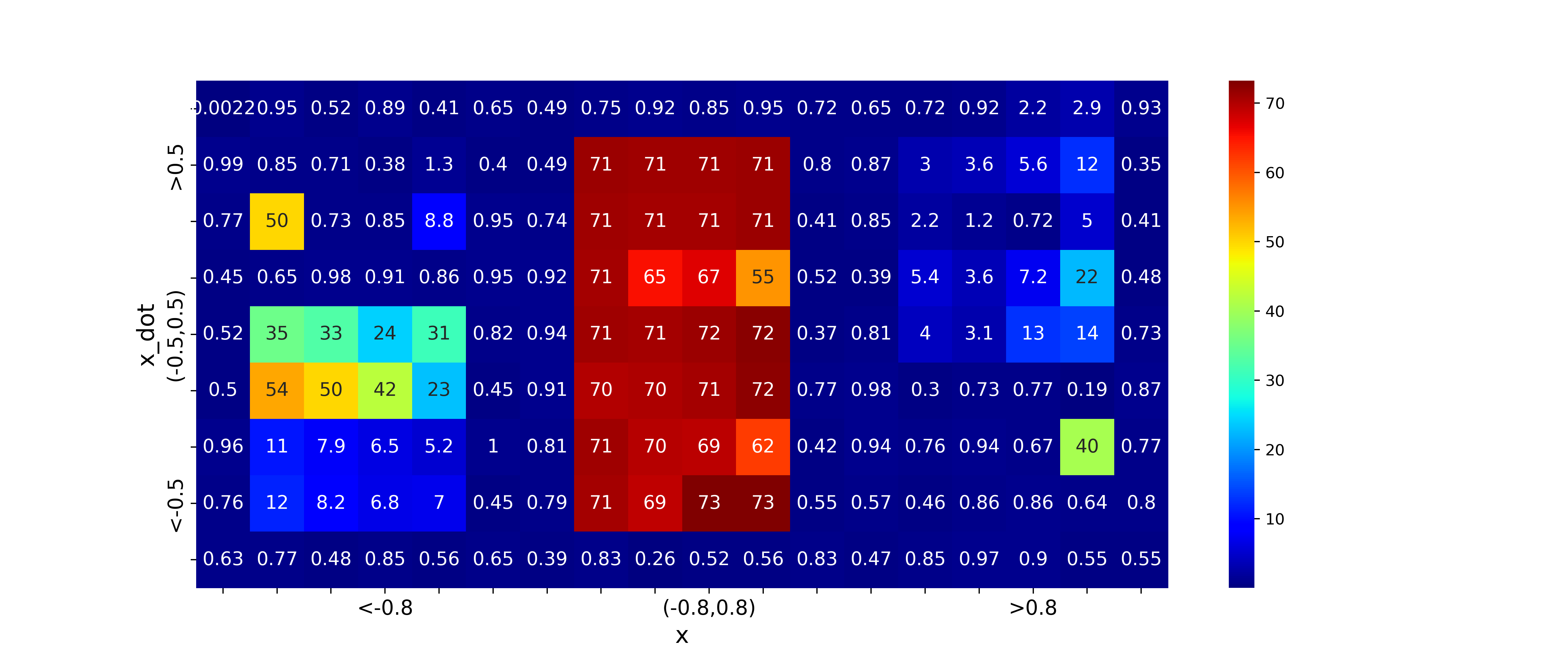
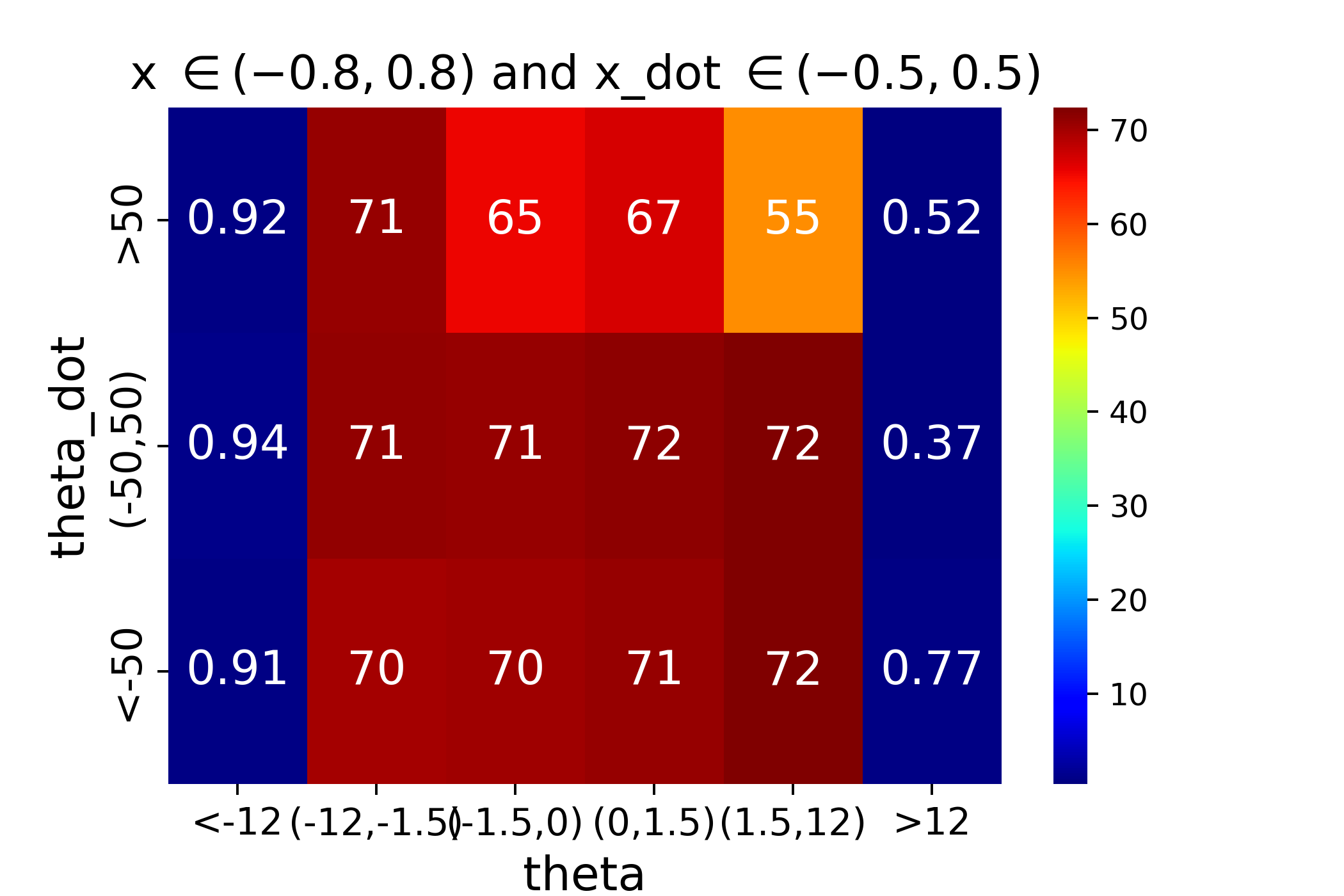
Q-learning implementation with box system:
import numpy as np
import gym
import random
def get_box(s):
x,x_dot,theta,theta_dot=s
if x < -.8:
box_idx = 0
elif x < .8:
box_idx = 1
else:
box_idx = 2
if x_dot < -.5:
pass
elif x_dot < .5:
box_idx += 3
else:
box_idx += 6
if theta < np.radians(-12):
pass
elif theta < np.radians(-1.5):
box_idx += 9
elif theta < np.radians(0):
box_idx += 18
elif theta < np.radians(1.5):
box_idx += 27
elif theta < np.radians(12):
box_idx += 36
else:
box_idx += 45
if theta_dot < np.radians(-50):
pass
elif theta_dot < np.radians(50):
box_idx += 54
else:
box_idx += 108
return box_idx
def e_greedy(q,epsilon,n_a):
if random.random()<epsilon:
a=np.random.randint(0,n_a)
else:
a=np.argmax(q)
return a
def run_qbox(n_eps=2000,n_stps=200,gm=0.99,lr=0.1,epsilon=1,epsilon_rate=0.995):
env=gym.make("CartPole-v0")
n_s=env.observation_space.shape[0]
n_a=env.action_space.n
Q=np.random.rand(162,n_a)
r_all,stp_all=[],[]
q_all=[]
for ep in range(n_eps):
s=env.reset()
s_int=get_box(s)
r_sum=0
for stp in range(n_stps):
q_all.append(Q[s_int])
a=e_greedy(Q[s_int],epsilon,n_a)
s_,r,done,_=env.step(a)
s_int_=get_box(s_)
delta=r+gm*np.max(Q[s_int_])-Q[s_int,a]
Q[s_int,a]+=lr*delta
s=s_
s_int=s_int_
r_sum+=r
if done:
break
r_all.append(r_sum)
stp_all.append(stp)
epsilon*=epsilon_rate
#if ep%(n_eps//5)==0 or ep==n_eps-1:
# print(f"ep:{ep}, stp:{stp}, r:{np.round(r_sum,2)},eps:{epsilon}")
return r_all,stp_all,q_all
r,s,q=run_qbox()
Q-bins
We could also divide the states in equal-distance bins with each state variables
Experimental setting:
- n_bins: number of bins for each state variables
- State space: (4,) continuous -> (n_bins^4,)
- exploration decaying rate (epsilon decay rate): 0.999
- others remain the same as in Q-box
def discretize(s,bins):
idx=[]
for i in range(n_s):
idx.append(np.digitize(s[i],bins[i])-1) # -1 will turn bin into index
return tuple(idx)
def run_qbin(n_bins=15,n_eps=2000,n_stps=200,gm=0.99,lr=0.1,eps=1,eps_decay=0.999):
env=gym.make('CartPole-v0')
n_a=env.action_space.n
n_s=env.observation_space.shape[0]
bins=[np.linspace(-2.4,2.4,n_bins),
np.linspace(-2,2,n_bins),
np.linspace(-.2618,.2618,n_bins),
np.linspace(-2,2,n_bins)]
#shape (n_bins,n_bins,n_bins,n_bins,n_a)
#i.e. (15,15,15,15,2)
Q=np.zeros(([len(bins[0])]*n_s+[n_a]))
r_all,stp_all,q_all=[],[],[]
for ep in range(n_eps):
r_sum,done=0,False
s_int=discretize(env.reset(),bins)
for stp in range(n_stps):
q_all.append(Q[s_int])
a=e_greedy(Q[s_int],eps,n_a)
s_,r,done,_=env.step(a)
s_int_=discretize(s_,bins)
delta=r+gm*np.max(Q[s_int_])-Q[s_int][a]
Q[s_int][a]+=lr*delta
s=s_
s_int=s_int_
r_sum+=r
if done:
break
eps*=eps_decay
if ep%(n_eps//10)==0 or ep==n_eps-1:
print(f"ep:{ep}, stp:{stp}, r:{np.round(r_sum,2)}, eps:{eps}")
r_all.append(r_sum)
stp_all.append(stp)
return r_all,stp_all,q_all
r,s,q=run_qbin(n_bins=15)
SARSA(λ)-rbf
We use RBF networks to approximate the Q function
RBF networks:
\[\begin{align*} \Phi_s(i)=\exp \left(-\frac{\|s-c_i\|^2}{2\sigma_i^2} \right) \end{align*}\]where \(c_i\) is the \(i\)th center point and \(\sigma_i\) is the \(i\)th standard deviation
Normalized RBF networks:
\[\begin{align*} \Phi_s(i)= \frac{\exp \left(-\frac{\|s-c_i\|^2}{2\sigma_i^2} \right)}{\sum_i \exp \left(-\frac{\|s-c_i\|^2}{2\sigma_i^2} \right)} \end{align*}\]RBF parameters:
- n_rbf: [3,3,5,5]
- n_feature: 3x3x5x5=225
- s_range_low: [-2.4,-4,-np.radians(30),-np.radians(180)]
- s_range_high: [2.4,4,np.radians(30),np.radians(180)]
RBF network plotted w.r.t the above parameters:
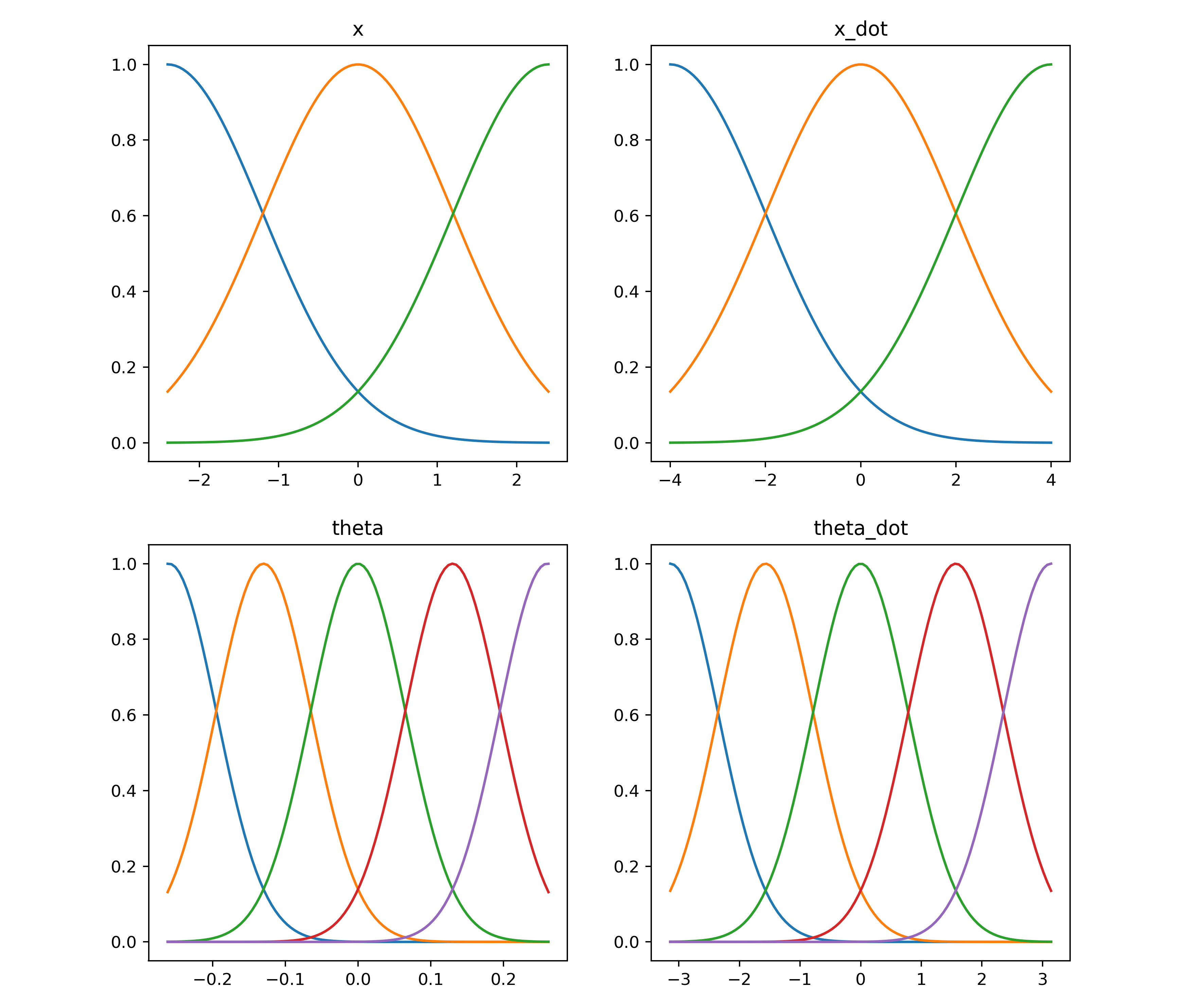
Experimental setting:
- State space to Feature space: (4,) continuous -> (225,) continuous
- eligibility trace factor (lmd): 0.5
- others remain the same as in Q-box
Customized Gym Env:
- In original gym env, state initialization is U(-0.05,0.05) for 4 states, this small range doesn’t encourage thorough state visits in terms of exploration, we changed it to U(-0.26,0.26) for 4 states (further can be changed to U(range of each state))
- also in self.theta_threshold_radians = 15 * 2 * math.pi / 360, 15 can be changed to 180 to test the property of continuous controller (further topic)
Learned optimal Values:
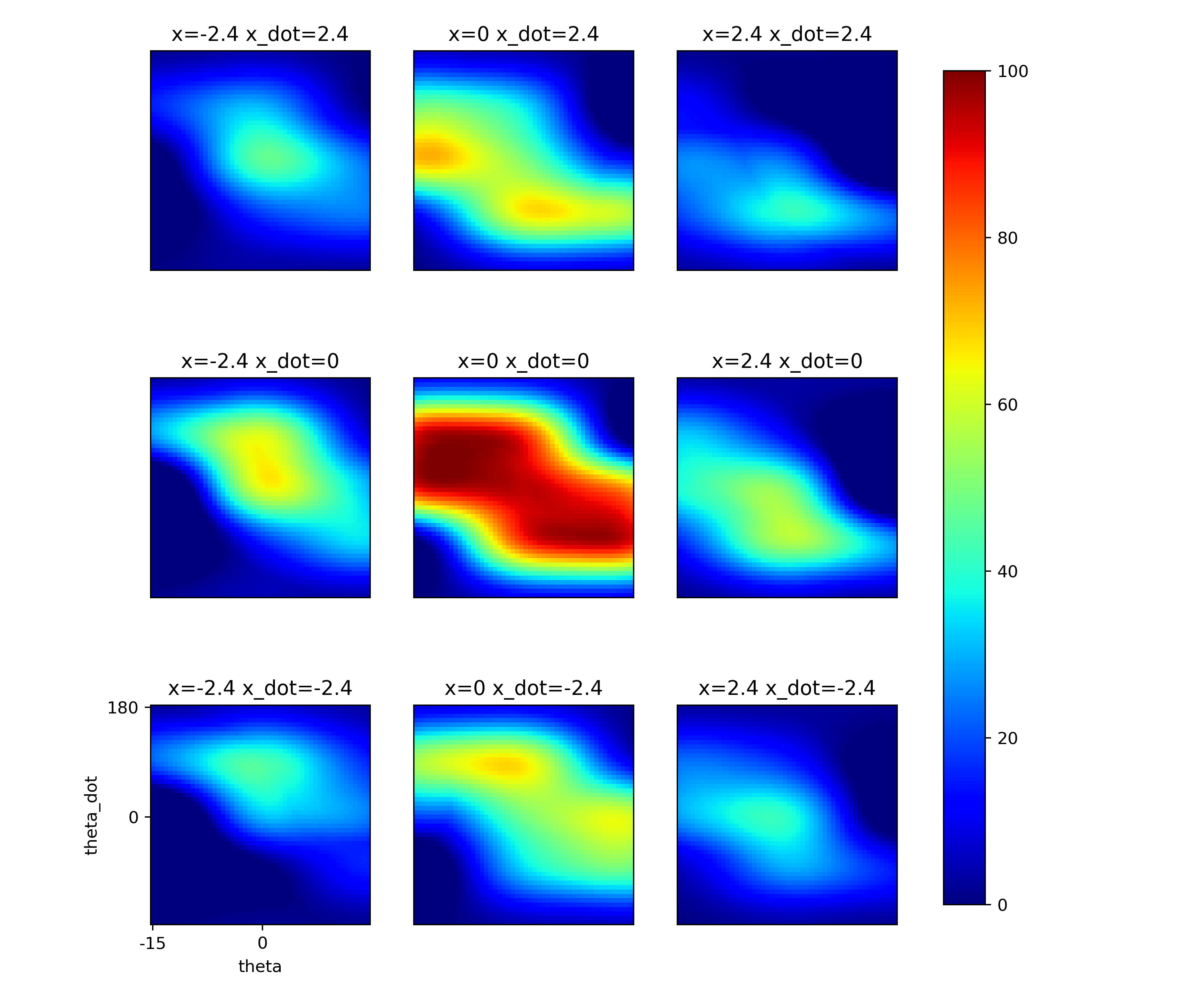
SARSA(λ) implementation:
import numpy as np
import pandas as pd
import gym
import math
import random
import matplotlib.pyplot as plt
def plot_rbf(s_range,center,sigma):
plt.figure(figsize=(10,10))
title=['x','x_dot','theta','theta_dot']
for i in range(1,5):
plt.subplot(2,2,i)
x=np.linspace(s_range[0,i-1],s_range[1,i-1],num=100)
y={}
for j in range(len(center[i-1])):
y[j]=np.exp(-(x-center[i-1][j])**2/(2*sigma[i-1]**2))
plt.plot(x,y[j])
plt.title(title[i-1])
plt.savefig('rbf.png',dpi=350)
def get_feature(s):
rbf={}
f=1 #feature
for i in range(4):
rbf[i]=np.exp(-(s[i]-center[i])**2/(2*sigma[i]**2))
f=np.outer(f,rbf[i])
f=f.ravel()
return f
def get_Q(F,w):
Q=np.dot(w.T,F)
return Q
def get_Q_a(F,a,w):
Q=np.dot(w[:,a],F)
def e_greedy(e,Q):
rand=np.random.random()
if rand<1.-e:
a=Q.argmax()
else:
a=env.action_space.sample()
return int(a)
def get_v(x,x_dot,w):
n_grid=50
v=np.zeros((n_grid,n_grid))
the=np.linspace(s_range[0,2]/2,s_range[1,2]/2,num=n_grid)
the_dot=np.linspace(s_range[1,3],s_range[0,3],num=n_grid)
for i in range(n_grid):
for j in range(n_grid):
s=np.array([x,x_dot,the[j],the_dot[i]])
F=get_feature(s)
v[i,j]=np.max(np.dot(w.T,F))
return v
def plot_v(w,angle=15,angular=229):
i=1
x_range=[-2.4,0,2.4]
x_dot_range=[-2,0,2]
plt.figure(figsize=(10,10))
for x_dot in reversed(x_dot_range):
for x in x_range:
v=get_v(x,x_dot,w)
plt.subplot(3,3,i)
plt.imshow(v,cmap='jet')
plt.colorbar()
plt.title('x='+str(x)+' x_dot='+str(x_dot))
plt.xticks(np.arange(50,step=25),('-'+str(angle),'0',))
plt.yticks(np.arange(50,step=25),(str(angular),'0',))
plt.xlabel('theta')
plt.ylabel('theta_dot')
i+=1
plt.savefig('q_op_rbf.png',dpi=350)
def initialize(env,n_s,n_a):
s_range=np.zeros((2,n_s))
s_range[0,:]=np.array([-2.4,-4,-np.radians(30),-np.radians(180)])
s_range[1,:]=np.array([2.4,4,np.radians(30),np.radians(180)])
n_rbf=np.array([3,3,5,5]).astype(int)
n_feature=np.prod(n_rbf)
w=np.zeros((n_feature,n_a))
interval={}
center={}
sigma={}
for i in range(n_s):
interval[i]=(s_range[1,i]-s_range[0,i])/(n_rbf[i]-1)
sigma[i]=interval[i]/2
center[i]=[np.around(s_range[0,i]+j*interval[i],2) for j in range(n_rbf[i])]
return s_range,center,sigma
def run_sarsalmd(n_eps=2000,n_stps=200,gm=0.99,lr=0.1,lmd=0.5,epsilon=1,epsilon_rate=0.995):
env=gym.make("CartPole-v0")
n_s=env.observation_space.shape[0]
n_a=env.action_space.n
s_range,center,sigma=initialize(env,n_s,n_a)
plot_rbf(s_range,center,sigma)
r_all,stp_all,q_all=[],[],[]
for ep in range(n_eps):
r_sum,done=0,False
#eligibility traces
e=np.zeros((n_feature,n_a))
F=get_feature(env.reset(),center,sigma)
Q_old=get_Q(F,w)
a=e_greedy(epsilon,Q_old)
for stp in range(n_stps):
#show animation of last 5 episodes
#if ep>n_eps-5:
# env.render()
q_all.append(Q_old)
s_,r,done,_=env.step(a)
F_=get_feature(s_,center,sigma)
Q=get_Q(F_,w)
a_=e_greedy(epsilon,Q)
if done:
delta=r-Q_old[a]
else:
delta=r+gm*Q[a_]-Q_old[a]
e[:,a]=F
for m in range(n_feature):
for n in range(n_a):
w[m,n]+=lr*delta*e[m,n]
e*=gm*lmd
s=s_
F=F_
a=a_
Q_old=Q
r_sum+=r
if done:
break
r_all.append(r_sum)
stp_all.append(stp)
epsilon*=epsilon_rate
#print(f"ep:{ep}, stp:{stp}, r:{np.round(r_sum,2)}, eps:{epsilon}")
plot_v(w)
return r_all,stp_all,q_all
r,s,q=run_sarsalmd()
DQN
We use deep neural network to approximate Q values
NN parameters:
- MLP layers: 3
- hidden units: 200 for each layer
- activator: relu
- state input: (4,)
- action output: (2,)
DQN Experimental setting:
- buffer size: 40000
- batch size: 512
- update target: every 10 episodes
- episode length: 3000
- step length: 1000
- lr: 0.001
- gm: 0.99
- eps: from 1.
- eps decay: 0.995
Customized Gym Env:
- the initial angle of pole ~ U(-15deg,15deg)
- end of episode [-30deg, 30deg]
Learned optimal Values:
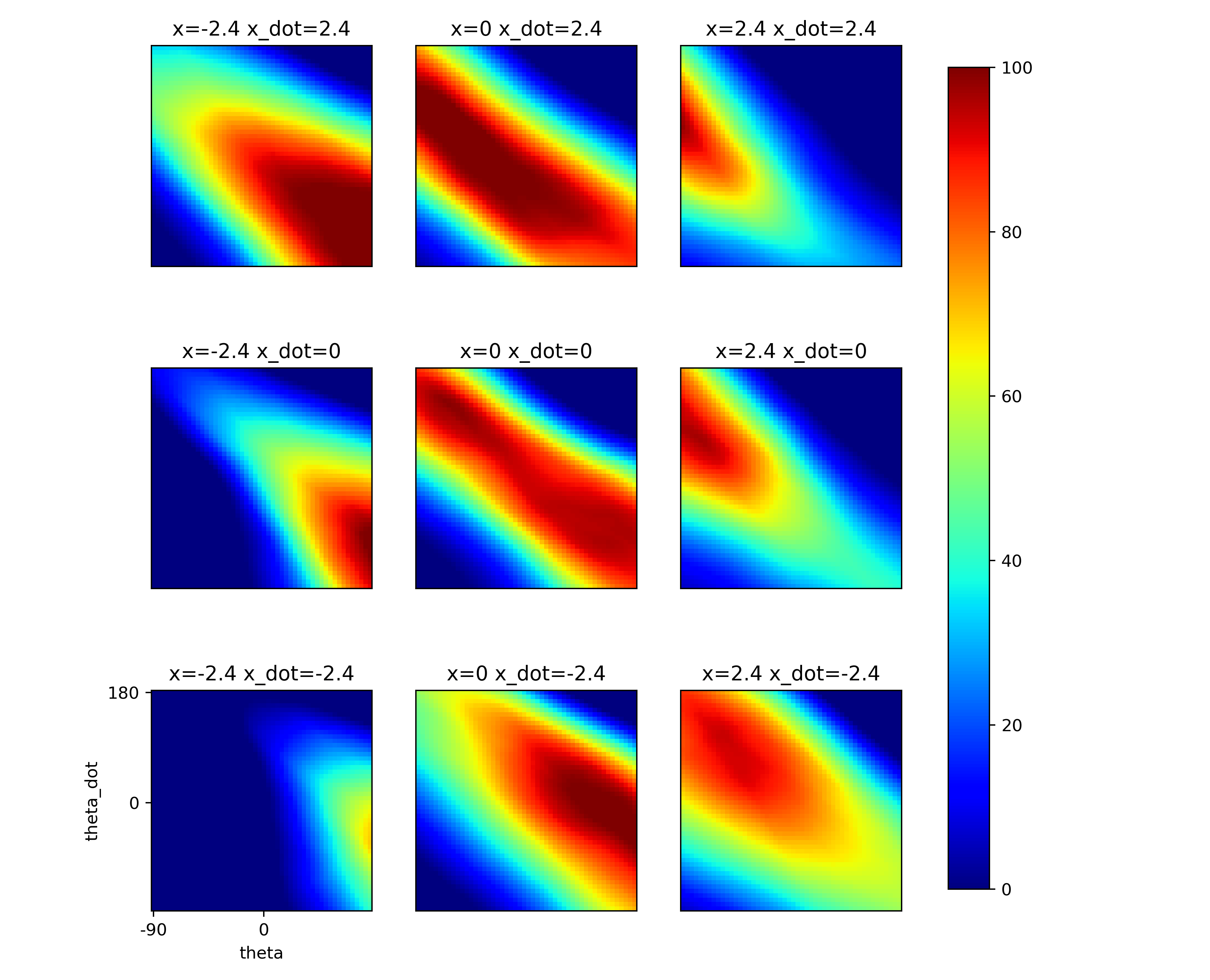
Implementation:
import random
import copy
import math
import numpy as np
import pandas as pd
from collections import deque
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
class DQN(nn.Module):
def __init__(self):
super().__init__()
self.fc1=nn.Linear(4, 200)
self.fc2=nn.Linear(200, 200)
self.fc3=nn.Linear(200, 200)
self.fc4=nn.Linear(200, 2)
def forward(self, x):
x=self.fc1(x)
x=F.relu(x) #SiLU
x=self.fc2(x)
x=F.relu(x)
x=self.fc3(x)
x=F.relu(x)
x=self.fc4(x)
return x
class NN:
def __init__(self,batch_size=32,buffer_size=2000,**kw):
self.batch_size=batch_size
self.buffer=deque(maxlen=buffer_size)
self.lr=kw['lr']
self.gm=kw['gm']
def initialize(self):
self.model,self.model_tar=self.create()
self.criterion=torch.nn.MSELoss()
self.opt=torch.optim.Adam(self.model.parameters(),lr=self.lr)
def create(self):
model=DQN()
model_tar=copy.deepcopy(model)
return model,model_tar
def update_target(self):
self.model_tar.load_state_dict(self.model.state_dict())
def update(self):
q_batch,q_tar_batch=[],[]
batch=random.sample(self.buffer,min(len(self.buffer),self.batch_size))
for s,a,r,s_, done in batch:
q=self.model(s)
q_tar=q.clone().detach()
with torch.no_grad():
q_tar[0][a]=r if done else r+self.gm*torch.max(self.model_tar(s_)[0])
q_batch.append(q[0])
q_tar_batch.append(q_tar[0])
q_batch=torch.cat(q_batch)
q_tar_batch=torch.cat(q_tar_batch)
self.opt.zero_grad()
loss=self.criterion(q_batch, q_tar_batch)
loss.backward()
self.opt.step()
return loss.item()
def add_memory(self,s,a,r,s_,done):
r=torch.tensor(r)
self.buffer.append((s,a,r,s_,done))
def get_q(self,s):
return self.model(s).detach().numpy()
def get_tar(self,s):
return self.model_tar(s).detach().numpy()
def save_model(self,pre):
torch.save(self.model.state_dict(), 'model_weights.pth')
class Agent:
def __init__(self,env,buffer_size,batch_size,update_tar,n_eps,n_stps,eps,eps_decay,**kw):
self.env=env
self.nn=NN(batch_size=batch_size,
buffer_size=buffer_size,
lr=kw['lr'],
gm=kw['gm'])
self.update_tar=update_tar
self.n_eps=n_eps
self.n_stps=n_stps
self.epsilon=eps
self.epsilon_decay=eps_decay
def train(self,n=5,save_result=False,save_model=False,record_q=False):
for i in range(n):
self.train_once(save_result=save_result,
save_model=save_model,
record_q=record_q,
prefix='n'+str(i))
def train_once(self,save_result=True,save_model=False,record_q=False,**kw):
r_all,stp_all,stpCnt=[],[],0
v_all,q_all=[],[]
self.nn.initialize()
for ep in range(self.n_eps):
r_sum,done=0,False
s=self.preprocess(self.env.reset())
ent=self.epsilon
for stp in range(self.n_stps):
if ep>self.n_eps-5:
self.env.render()
q=self.nn.get_q(s)
a=self.e_greedy(s,ent)
if record_q:
q_all.append(q[0])
s_,r,done,_=self.env.step(a)
s_=self.preprocess(s_)
self.nn.add_memory(s,a,r,s_,done)
s=s_
r_sum+=r
stpCnt+=1
if done:
break
if ep%self.update_tar==0:
self.nn.update_target()
print('Target Updated!')
loss=self.nn.update()
self.epsilon*=self.epsilon_decay
print("Ep:"+str(ep)+" Stps:"+str(stp)+" R:"+str(r_sum)+" loss:"+str(loss)+" ent:"+str(ent))
r_all.append(np.round(r_sum,2))
stp_all.append(stp)
self.env.close()
if save_result:
pre=kw['prefix']
result=pd.DataFrame(zip(stp_all,r_all),columns=['step','return'])
result.to_csv(pre+'_result.csv',index=False)
if record_q:
pre=kw['prefix']
np.save(pre+'_q.npy',q_all)
if save_model:
pre=kw['prefix']
self.nn.save_model(pre)
def preprocess(self,s):
return torch.tensor(np.reshape(s, [1, 4]), dtype=torch.float32)
def e_greedy(self, s, epsilon):
if (np.random.random() <= epsilon):
return self.env.action_space.sample()
else:
with torch.no_grad():
return torch.argmax(self.nn.model(s)).numpy()
def main():
agt=Agent(env=gym.make('CartPole-v0'),
buffer_size=40000,
batch_size=512,
update_tar=10,
n_eps=2000,
n_stps=200,
eps=1.0,
eps_decay=0.995,
lr=0.001,
gm=0.99,)
agt.train(n=1,
save_result=True,
save_model=True,
record_q=True)
if __name__ == '__main__':
main()
REINFORCE and baseline
We directly learn a linear parameterized Gaussian policy, which is different from epsilon-greedy policy derived from a learned value function in the above methods
\[\pi(a \mid s, \boldsymbol{\theta})=\mathcal{N}(\textbf{w}^T X, \left[\exp(\textbf{w}^T X)\right]^2)\]where \(X=[x,\dot{x},\theta,\dot{\theta}]^T\)
Note:
-
since Gaussian policy is a stochastic policy, the exploration is done in the parameter space with the Gaussian variance \(\sigma^2\)
-
REINFORCE requires the policy to be differentiable and we have to manually derive the log derivative of the policy for gradient updating
-
we simply use an average-return baseline
See this post for more details Policy Gradient and Actor Critic
Customized Gym Env:
The continuous action env is from this link
Experimental setting:
- State space: (4,) continuous
- Action sapce: (1,) continuous
- learning rate (lr): 0.0001
- others remain the same as in Q-box
def Gaussian_policy(w_mu,w_sig,s):
mu=w_mu.T.dot(s)[0]
upper=w_sig.T.dot(s)
sig=np.exp(upper-np.max(upper))[0]
return np.random.normal(mu,sig)[0],mu[0],sig[0]
def get_dlog(mu,sig,s,a):
dlog_mu=((a-mu)/(sig**2))*s
dlog_sig=(((a-mu)**2/sig**2)-1)*s
return dlog_mu,dlog_sig
def get_return(rewards,gm):
R=np.zeros(len(rewards))
R[-1]=rewards[-1]
for i in range(2,len(R)+1):
R[-i]=gm*R[-i+1]+rewards[-i]
return R
def run_reinforce(n_eps=2000,n_stps=200,gm=0.99,lr=0.0001,baseline=False):
from env_continuous import ContinuousCartPoleEnv
env=ContinuousCartPoleEnv()
w_mu=np.zeros((4,1))
w_sig=np.zeros((4,1))
r_all,s_all=[],[]
for ep in range(n_eps):
stp,r_sum,done=0,0,False
states,actions,rewards,mus,sigs=[],[],[],[],[]
s=env.reset().reshape((4,1))
for stp in range(n_stps):
a,mu,sig=Gaussian_policy(w_mu,w_sig,s)
s_,r,done,_=env.step(a)
s_=s_.reshape((4,1))
states.append(s)
actions.append(a)
rewards.append(r)
mus.append(mu)
sigs.append(sig)
s=s_
stp+=1
if done:
break
R=get_return(rewards,gm)
#update policy parameters
gmt=1
for i in range(len(rewards)):
dlog_mu,dlog_sig=get_dlog(mus[i],sigs[i],states[i],actions[i])
if baseline:
w_mu=w_mu+lr*gmt*(R[i]-sum(R)/len(R))*dlog_mu
w_sig=w_sig+lr*gmt*(R[i]-sum(R)/len(R))*dlog_sig
else:
w_mu=w_mu+lr*gmt*(R[i])*dlog_mu
w_sig=w_sig+lr*gmt*(R[i])*dlog_sig
gmt*=gm
#if ep%(n_eps//10)==0:
# print(f'ep:{ep}, R:{sum(rewards)}, stp:{stp}')
r_all.append(sum(rewards))
s_all.append(stp)
return r_all,s_all
r_rf,s_rf=run_reinforce(baseline=False)
r_rfb,s_rfb=run_reinforce(baseline=True)
References
[Barto et al. 1983] Barto, Andrew G., Richard S. Sutton, and Charles W. Anderson. “Neuronlike adaptive elements that can solve difficult learning control problems.” IEEE transactions on systems, man, and cybernetics 5 (1983): 834-846.
[PILCO 2011] Deisenroth, Marc, and Carl E. Rasmussen. “PILCO: A model-based and data-efficient approach to policy search.” Proceedings of the 28th International Conference on machine learning (ICML-11). 2011.
[Michie et al. 1968] Michie, Donald, and Roger A. Chambers. “BOXES: An experiment in adaptive control.” Machine intelligence 2.2 (1968): 137-152.
[Doya 2000] Doya, Kenji. “Reinforcement learning in continuous time and space.” Neural computation 12.1 (2000): 219-245.