Multitask Robust RL
Intro
Innovations introduced to improve
- wall clock time
- data efficiency
- robustness
(1) by changing the learning algorithm:
- Prioritized experience replay
- Double Q learning
(2) by improving the optimizer:
- A3C
- TRPO
(3) or whereby data efficiency is improved by training additional auxiliary tasks jointly with the RL task:
- RL with unsupervised auxiliary tasks
- Playing FPS games with DRL
- Learning to navigate in complex environment
to solve complex tasks either simultaneously or sequentially, it requires robust algs which
- do not rely on task-specific algorithmic design
- or do not rely on extensive hyperparameter tuning
this intuition has long been pursued in multitask and transfer-learning
- Deep learning of representations for unsupervised and transfer learning [Yoshua Bengio 2012]
- Multitask learning [Rich Caruana 1997]
- An introduction to inter-task transfer for reinforcement learning [Taylor and Stone 2011]
- How transferable are features in deep neural networks? [Yosinski et al 2014]
However, transfer learning poses additional challenges to exsiting methods:
- Actor-mimic: Deep multitask and transfer reinforcement learning [ICLR 2016]
- Policy distillation [ICLR 2016]
- Revisiting natural gradient for deep networks [ICLR 2014]
It is likely that gradients from other tasks behave as noise, interfering with learning, or one of the tasks might dominate the others
what is data efficiency in machine learning?
- the ability to learn in complex domains without requiring large quantities of data
Distral
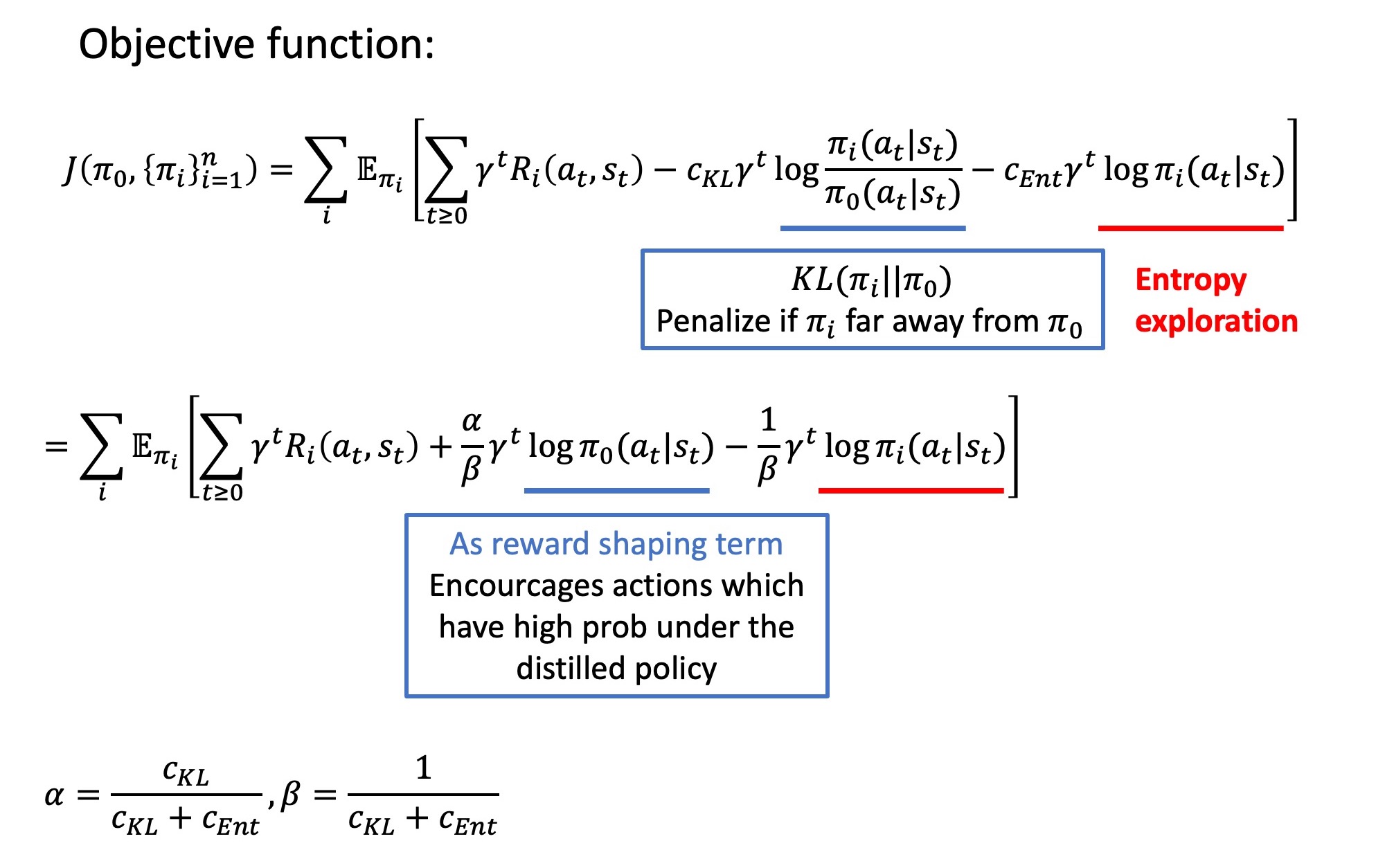


The learning procedure:



Distilled Policies
[5] model compression KDD 2006
[11] distilling the knowledge in a neural network NIPS 2014
[19] Actor-mimic: deep multitask and transfer RL ICLR 2016
[22] Policy distillation ICLR 2016
Policy Distillation
policy distillation for transferring one or more action policies from Q-networks to an untrained network
(+) network size can be compressed by up to 15 times without degradation in performance
(+) multiple expert policies can be combined into a single multi-task poliy that can outperform the original experts
(+) it can be applied as a real-time, online learning process by continually distilling the best policy to a target network, thus efficiently tracking the evolving Q-learning policy
intro of distillation
- an effcient means for supervised model compression [Bucila et al 2006]
- creating a single network from an ensemble model [Hinton et al 2014]
- an optimization method that acts to stabilize learning over large datasets or in dynamic domains [Shalev-Shwartz 2014]
Distillation uses supervised regression to train a target network to produce the same output distribution as the original network, often using a less peaked, or ‘softened’ target distribution
distillation related research topic:
model compression using distillation
deep RL
multi-task learning
imitation learning
Distillation is a method to transfer knowledge from a Teacher model to a Student model
T->S
How to transfer Q-values and its difficulty
- the scale of the Q-values may be hard to learn because it is not bounded and can be quite unstable
- it is computationally challenging in general to comput the action values of a fixed policy because it implies solving the Q-value evaluation problem
- training S to predict only the single best action is also problematic, since there may be multiple actions with similar Q-values
3 methods from T->S
in all cases, we assume that the T has been used to generate a dataset
D^T={(s_i,q_i)}^N
s_i - a short observation sequence
q_i - a vector of unnormalized Q-values with one value per action
Method 1: uses only the highest valued action from the teacher a_i,best=argmax(q_i), the S is trained with a negative log likelihood loss (NLL) to predict the same action:
|D|
L_{NLL}(D^T,θ_S) = - Σ log P(a_i=a_i,best|x_i,θ_S)
Method 2: uses a mean-squared-error loss, it preserves the full set of action-values in the resulting student model:
|D|
L_{MSE}(D^T,θ_S) = Σ ||q_i^T-q_i^s||_2^2
q^T - the vectors of Q-values from the teacher networks
q^S - the vectors of Q-values from the student networks
Method 3: uses KL divergence with temperature τ, the outputs of the teacher are the expected future discounted reward of each possible action so we may need to make them sharper (smaller τ)
|D| q_i^T softmax(q_i^T/τ)
L_{KL}(D^T,θ_S) = Σ softmax(-----) ln ----------------
τ softmax(q_i^S)
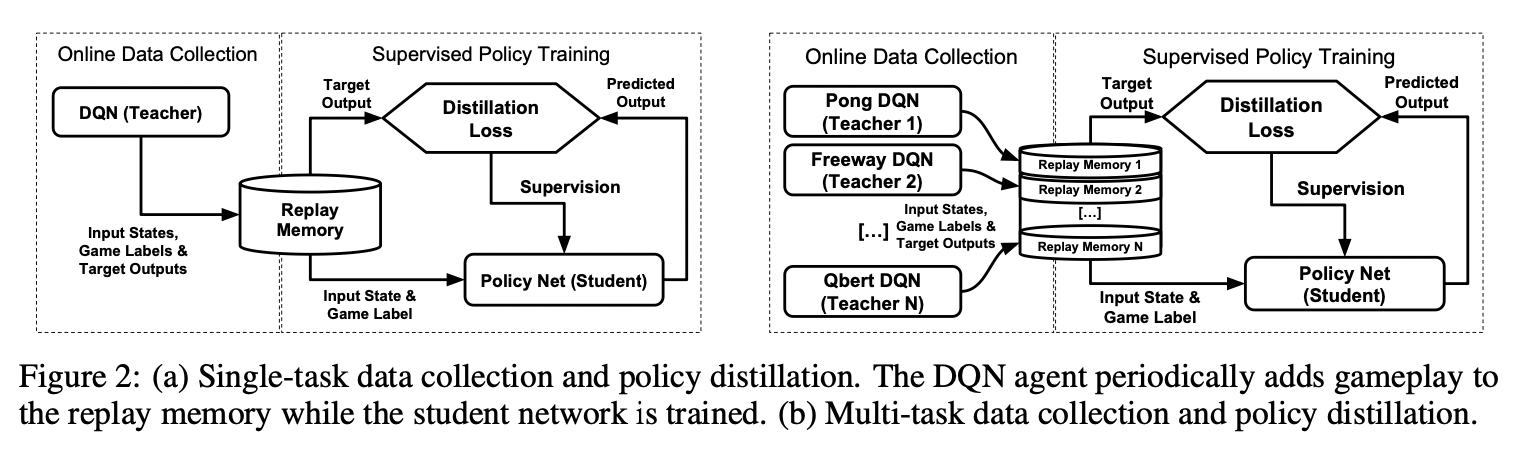
Multi-task DQN VS Multi-task distillation agents:
experimental setting:
- game is switched every episode (game label used)
- separate replay buffers are maintained for each task
- training is evenly interleaved among all tasks
failure of DQN:
- due to interference between the different polices, different reward scaling, and the inherent instability of learning value functions
advantage of policy distillation:
- it may offer a means of combining multiple polices into a single network without the damaging interference and scaling problems
- since policies are compressed and refined during the distillation process, we surmise that they may also be more effectively combined into a single network
- policies are inherently lower variance thatn value functions, which should help performance and stability [Variance reduction techniques for gradient estimates in reinforcement learning 2004]
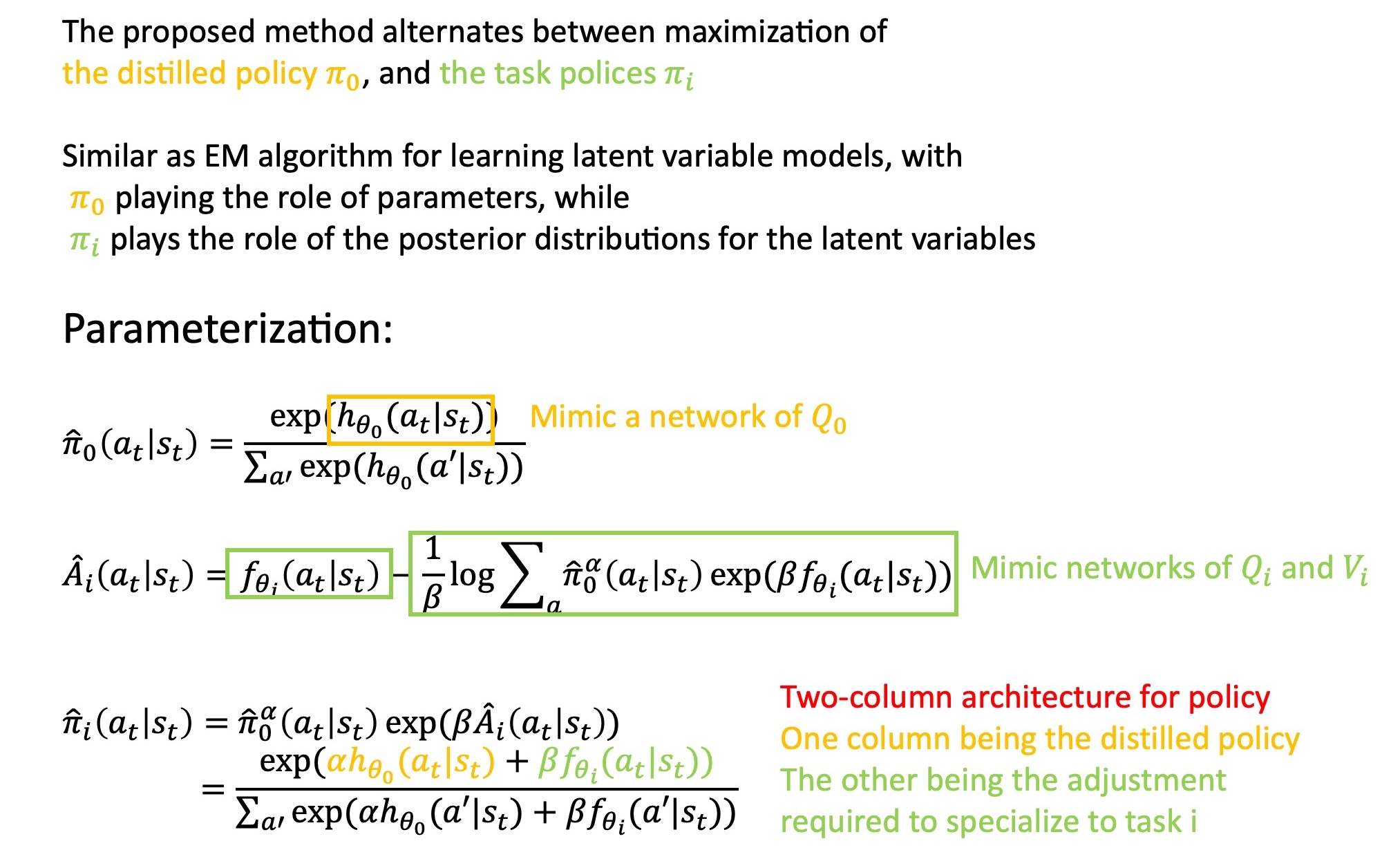
Actor-Mimic
DRL + model compression => generalize its knowledge to new domains
Actor-Mimic leverages techniques from model compression to train a single multitask network using guidance from a set of game-specific expert networks
For transfer learning, treat a multitask network as being a DQN which was pre-trained on a set of source tasks
the replay memory is used to reduce correlations between adjacent states and is shown to have large effect on the stability of training the network in some games
it’s difficult to directly distill knowledge from the expert value functions, instead, match policies by first transforming Q-values using a softmax
(+) softmax gives us outputs which are bounded in the unit interval and so the effects of the different scales of each expert’s Q-function are diminished, achieving higher stability during learning
step 1: transform each expert DQN into a policy network by a Boltzmann distribution defined over the Q-value outputs
exp(Q_Ei(s,a)/τ)
π_Ei (a|s) = ---------------------- a'∈A_Ei
Σ_a' exp(Q_Ei(s,a')/τ)
step 2: define the policy objective over the multitask network as the cross-entropy between the expert network’s policy and the current multitask policy <- policy regression loss
L^i_policy (θ) = Σ_a π_Ei(a|s) log π_AMN(a|s;θ) a∈A_Ei
π_AMN(a|s;θ) - the multitask Actor-Mimic Network policy parameterized by θ
in contrast to the Q-learning objective which recursively relies on itself as a target value, we now have a stable supervised training signal (the excpert network output) to guide the multitask network
sampling can be either from the expert network or the AMN action outputs, empirically, the latter was better
h_AMN(s) - the hidden activations in the feature layer of the AMN
h_Ei(s) - the hidden activations in the feature layer of the i'th expert network computed from the input state s
the dimension of h_AMN(s) does not necessarily need to be equal to h_Ei(s)
f_i(h_AMN(s)) - a feature regression network, for a given state s, attempts to predict the features h_Ei(s) from h_AMN(s)
L^i_feature (θ,θ_fi) = ||f_i(h_AMN(s;θ);θ_fi)-h_Ei(s)||^2_2
Actor-Mimic:
L^i_actormimic (θ,θ_fi) = L^i_policy + β L^i_feature (θ,θ_fi)
β - scaling parameter controls the relative weighting of the two objectives
we can think of the policy regression obj as
- a teacher (expert network) telling a student (AMN) how they should act (mimic expert’s actions)
while the feature regression obj as
- a teacher telling a student why it should act that way (mimic expert’s thinking process)
Convergence
[A convergent form of approximate policy iteration NIPS 2002]
[A reduction of imitation learning and structured prediction to no-regret online learning JMLR 2011]
DAAP - Dynamic Actor-Advisor Programming
safe RL
[12] J. García and F. Fernández, “A comprehensive survey on safe rein- forcement learning,” Journal of Machine Learning Research (JMLR), vol. 16, pp. 1437–1480, Jan. 2015
[7] J.Garcia and F.Fernandez, “Safe exploration of state and action spaces in reinforcement learning,” Journal of Artificial Intelligence Research, vol. 45, pp. 515–564, 2012
[8] Z. C. Lipton, J. Gao, L. Li, J. Chen, and L. Deng, “Combating reinforcement learning’s sisyphean curse with intrinsic fear,” CoRR, vol. abs/1611.01211, 2016
Constrained-MDP
[20] H. Plisnier, D. Steckelmacher, D. M. Roijers, and A. Nowé, “The actor-advisor: Policy gradient with off-policy advice,” CoRR, vol. abs/1902.02556, 2019
Reference
[1] Teh, Yee Whye, et al. “Distral: Robust multitask reinforcement learning.” arXiv preprint arXiv:1707.04175 (2017)
[22] Policy distillation ICLR 2016
[19] Actor-mimic: deep multitask and transfer RL ICLR 2016
[?] Dynamic Actor-Advisor Programming for Scalable Safe RL ICRA 2020
ICML 2016 Workshop on Data-Efficient Machine Learning
cross entropy ml-cheatsheet
Computing Stationary Distributions of a Discrete Markov Chain
Stationary Distributions of Markov Chains
