Data Structure 9 - tree
Background
Definition
A tree is a widely used abstract data type that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the “children”), with the constraints that no reference is duplicated, and none points to the root.
Alternatively, a tree can be defined abstractly as a whole (globally) as an ordered tree, with a value assigned to each node.
Edge - connection between one node to another
Path - a sequence of nodes and edges connecting a node with a descendant
- includes all nodes and all edges along the path
- the direction of a path is strictly from top to bottom and cannot be changed in middle
Height might have two definition based on different text books
Height 1 - the number of edges on the longest downward path between that node and a leaf (top-down)
- every node has height
- the height of a tree with single node is 1
- leaf cannot have height as there will be no path starting from a leaf
- the height of a tree is the number of edges on the longest downward path between the root and a leaf
- the height of a tree is the height of the root
-
the height of one node is the longest path from the node to a leaf, i.e. A’s height is 3 from A to E (number of edges)
A - level 1 / \ B C - level 2, depth of nodes = 1 / / \ G D F - level 3, depth of nodes = 2 / E - level 4, depth of nodes = 3
Height 2 - the number of nodes on its longest branch, a path from root to a leaf
Depth - the number of edges from the node to the tree’s root node (bottom-up)
- nothing to do with path, just count the edges between the targeting node and the root, ignoring directions
- the depth of the root is 0
Level - the level of a node is defined by 1 + the number of connections between the node and the root (bottom-up)
- level=depth+1
- level of root is 1
Full Binary Tree - a binary tree in which each node has exactly zero or two children
Complete Binary Tree - a completely filled binary tree with the possible exception of the bottom level, which is filled from left to right. It can have between 1 and 2^l nodes inclusive at the last level l.
Perfect Binary Tree - a binary tree that is full and complete, perfect tree has 2^l-1 nodes, where l is the number of levels
0 0 0 0 0
/ \ / \ / \ / \ / \
1 2 1 2 1 2 1 2 1 2
/ \ / \ \ / \ / / / \ / \
3 4 3 4 5 3 4 5 3 3 4 5 6
full & not full & complete complete perfect
complete not complete
Balanced Tree - a tree where every leaf is “not more than a certain distance” away from the root than any other leaf, normally the distance is set to 1
- “balanced” doesn’t mean the left and right subtrees are exactly the same tree
- “balanced” means not terribly imbalanced, balanced enough to ensure TO(logn) for insert and find
An AVL tree or a Red-black tree are common balanced trees
Properties
A - level 1
/ \
B C - level 2, max number of nodes = 2^(2-1)=2
/ / \
G D F - level 3, max number of nodes = 2^(3-1)=4
/
E - level 4, max number of nodes = 2^(4-1)=8
- The max number of nodes at lever l is 2^(l-1)
- A binary tree with n leaves has at least log2(n)+1 levels
- The max number of nodes in a binary tree of height h is
2^h-1, when the height of the root is considered as 1
2^(h+1)-1, when the height of the root is considered as 0 - A binary tree with n nodes has minimum possible height or minimum number of levels as
log2(n+1), if the height of a leaf node is considered as 1
log2(n+1)-1, if the height of a leaf node is considered as 0 - In a binary tree where every node has 0 or 2 children, number of leaf nodes is alway one more then nodes with two children
L=T+1
L - number of leaf nodes
T - number of internal nodes with two children
Points to Note
- tree VS binary tree
- binary tree VS binary search tree, bst equality?, can have dups?
- balanced VS unbalanced
Basic Operations
- insert() - TO(n)
- delete() - TO(n), can be TO(logn)??
- find() - TO(n)
- print() - TO(n)
- height() - TO(), every node has height, number of edges to the farthest leaf, top-down
- depth() - TO(), number of edges to the root, bottom-up
- level() - TO(), depth()+1, bottom-up
- maxDepth() - TO(n), longest path from root to farthest leaf
- minDepth() - TO(n), shortest path from root to nearest leaf
- size() - TO(n), total number of nodes
- isFull()
- isComplete()
- isPerfect()
- isBalanced() - TO(n)
- inOrder() - TO(n), dfs traversal
- preOrder() - TO(n), dfs traversal
- postOrder() - TO(n), dfs traversal
- levelOrder() - TO(n), bfs traversal
Implementation
class TreeNode():
def __init__(self,x):
self.val=x
self.left=None
self.right=None
#create tree
root=TreeNode(0)
root.left=TreeNode(1)
root.right=TreeNode(2)
root.left.left=TreeNode(3)
root.right.left=TreeNode(4)
- insert
- delete
- find
class BinaryTree():
def __init__(self):
self.root=None
def insert(self,data):
if not self.root:
self.root=TreeNode(data)
else:
self._insert(data,self.root)
def _insert(self,data,node): #node <- root
if data<node.data:
if not node.left:
node.left=TreeNode(data)
else:
self._insert(data,node.left)
else:
if not node.right:
node.right=TreeNode(data)
else:
self._insert(data,node.right)
def find(self,data):
if not self.root:
return None
else:
return self._find(data,self.root)
def _find(self,data,node):
if data==node.data:
return node
elif data<node.data and node.left:
self._find(data,node.left)
elif data>node.data and node.right:
self._find(data,node.right)
def print(self): #in order
if self.root:
self._print(self.root)
def _print(self,node):
if node:
self._print(node.left)
print(node.data)
self._print(node.right)
def deleteTree(self):
self.root=None
bt=BinaryTree()
bt.insert(3)
bt.insert(4)
bt.insert(0)
bt.insert(8)
bt.insert(2)
bt.print() #inorder
>>
0
2
3
4
8
bt.find(3).data
>>3
bt.find(10)
>>None
bt.deleteTree()
bt.print()
>>
- max depth - leetcode 104 - Maximum Depth of Binary Tree [E]
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example:
Given binary tree [3,9,20,null,null,15,7], return its depth = 3.
3
/ \
9 20
/ \
15 7
maxD(3)
| 3*
1+max(maxD(9), maxD(20))
1 | \ 2*
1+max(maxD(N),maxD(N)) 1+max(maxD(15), maxD(7))
1 | \ 1
1+max(maxD(N),maxD(N)) 1+max(maxD(N),maxD(N))
def maxDepth(self, root):
if not root:
return 0
return 1+max(self.maxDepth(root.left),self.maxDepth(root.right))
- min depth - leetcode 111 - Minimum Depth of Binary Tree [E]
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
3
/ \
9 20
/ \
15 7
minD(3)
| 2*
1+min(minD(9), minD(20))
| 1* \ 2
no 9.left \
1+minD(9.right) 1+min(minD(15), minD(7))
| 0 | 1 \ 1
no 9.right no 15.left no 7.left
| 1 \ 1
1+minD(15.right) 1+minD(7.right)
| 0 \ 0
no 15.right no 7.right
def minDepth(self, root):
if not root:
return 0
if not root.left:
return 1+self.minDepth(root.right)
if not root.right:
return 1+self.minDepth(root.left)
return 1+min(self.minDepth(root.left),self.minDepth(root.right))
- size
if a node doesn’t have children return 1
number of subtree nodes = size(root)+size(leftchild)+size(rightchild): 1+size(node.left)+size(node.right)
3
/ \
9 20
/ \
15 7
s(3)
| 5
1+s(9)+s(20)
| 1 \ 3
no children 1+s(15)+s(7)
1 1
def size(self, root):
if not root:
return 0
if not root.left and not root.right:
return 1
return 1+self.size(root.left)+self.size(root.right)
- size of complete tree - leetcode 222 - Count Complete Tree Nodes [M]
Given a complete binary tree, count the number of nodes.
Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2^h nodes inclusive at the last level h.
Input:
1
/ \
2 3
/ \ /
4 5 6
Solution 1: TO((logn)^2) SO(1)
Complete Tree property: except the last level, above l-1 is a perfect tree, node number= 2^l
- compare depths of left and right nodes of root
if left depth==right depth means, left sub is full, and right sub tree has one child or two, count the left sub tree nodes first with 2^left_depth, then count right sub tree with recursion
if left depth!=right depth means, left sub has one child or two, right sub is None, count the right sub tree first with 2^right_depth, then count left sub tree with recursion
1 1
/ \ / \
2 3 2 3
/ \ / \ /
4 5 4 5 6
ld(2)!=rd(3) ld(2)==rd(3)
2 1 2 2
=>rightsub is None =>leftsub is full
can calculate at first can calculate at first
size(1,3)=2 size(1,2,4,5)=4
countN(1) ld(2)!=ld(3) countN(1) ld(2)==rd(3)
| 5* / | 6* /
2**rd+countN(2) ld(4)==rd(5) 2**ld+countN(3) ld(6)!=rd(N)
2**1 | 3 / 2**2+ | 2 /
2**ld+countN(5) ld(N)==rd(N) 2**rd+countN(6) ld(N)==rd(N)
2**1 | 1 / 2**0 | 1 /
2**ld+countN(N) 2**ld+countN(N)
2**0 0 2**0+0
class Solution():
def countNodes(self,root):
if not root:
return 0
left_dep=self.depth(root.left)
right_dep=self.depth(root.right)
if left_dep==right_dep:
return 2**left_dep+self.countNodes(root.right)
else:
return 2**right_dep+self.countNodes(root.left)
def depth(self,node):
depth=0
while node:
node=node.left
depth+=1
return depth
Solution 2 - binary search see binary search #count tree nodes
- is balanced tree - leetcode 110 - Balanced Binary Tree [E]
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
Given the following tree [3,9,20,null,null,15,7]: return True
3
/ \
9 20
/ \
15 7
Example 2:
Given the following tree [1,2,2,3,3,null,null,4,4]: return False
1
/ \
2 3
/ \
4 5
/ \
6 7
Solution:
- need to know the height, equivalent to max_depth
- compare the height of left and right
class Solution1(): #easy to understand
res=True
def isBalanced(self,root):
self.height(root)
return self.res
def height(self,node): #equal to max_depth leetcode 104
if not node or not self.res:
return 0
if abs(self.height(node.left)-self.height(node.right))>1:
self.res=False
return 1+max(self.height(node.left),self.height(node.right))
class Solution2(): #TO(n) kind of optimized
def isBalanced(self, root):
return self.dfs(root)!=-1
def dfs(self,node):
if not node:
return 0
left_depth=self.dfs(node.left)
right_depth=self.dfs(node.right)
if left_depth==-1 or right_depth==-1:
return -1
if abs(left_depth-right_depth)>1:
return -1
return 1+max(left_depth,right_depth) # for calculating max depth
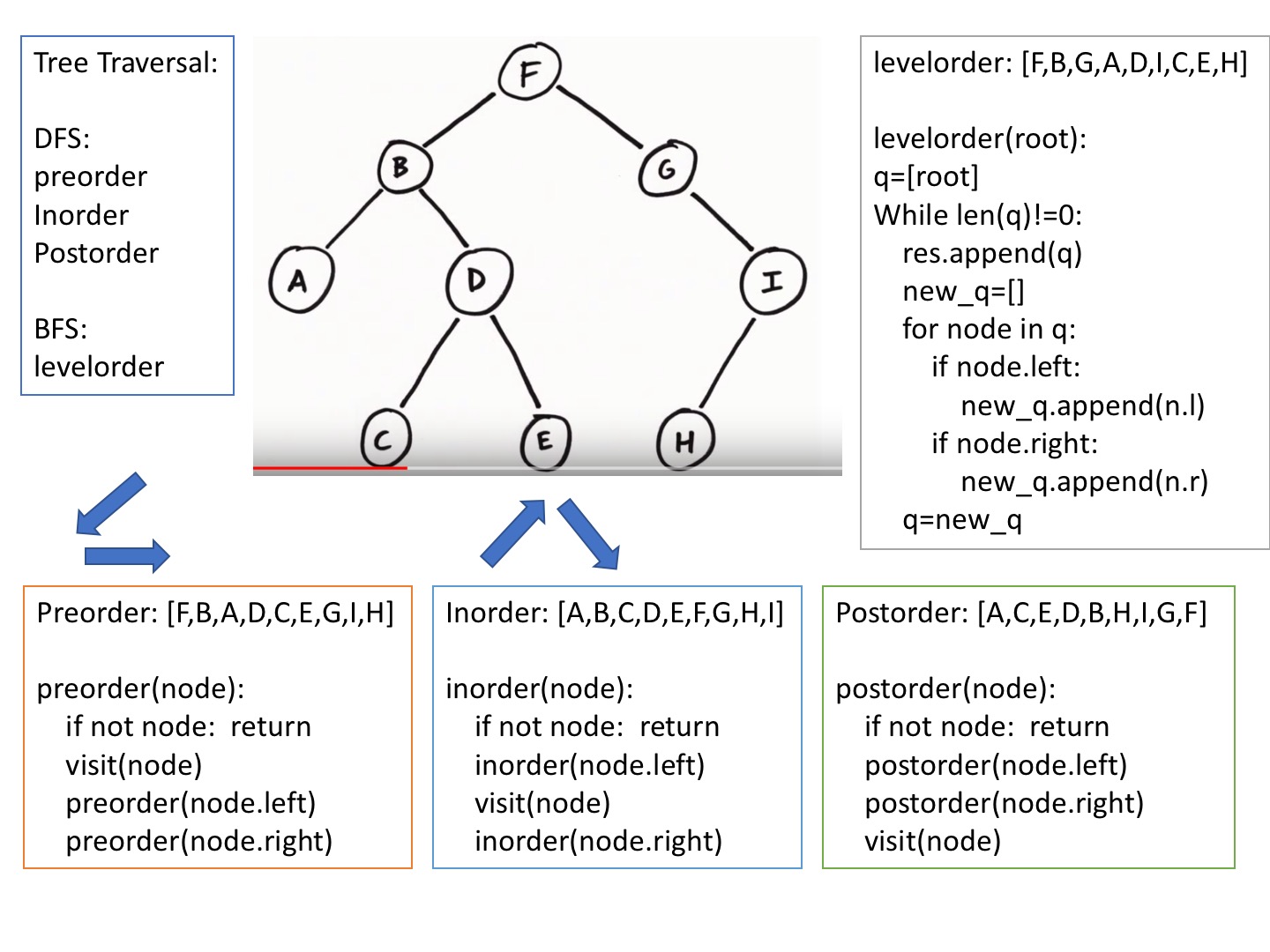
Traversal
DFS - inorder, preorder and postorder
BFS - levelorder
leetcode 94 - Binary Tree Inorder Traversal [M]
leetcode 144 - Binary Tree Preorder Traversal [M]
leetcode 145 - Binary Tree Postorder Traversal [H]
class BinaryTreeTraversal1():
#leetcode 94
def inorder(self,root):
res=[]
self.dfs(root,res)
return res
def dfs(self,node,res):
if not node:
return
self.dfs(node.left,res)
res.append(node.val)
self.dfs(node.right,res)
class BinaryTreeTraversal2():
#leetcode 144
def preorder(self,root):
res=[]
self.dfs(root,res)
return res
def dfs(self,node,res):
if not node:
return
res.append(node.val)
self.dfs(node.left,res)
self.dfs(node.right,res)
class BinaryTreeTraversal3():
#leetcode 145
def postorder(self,root):
res=[]
self.dfs(root,res)
return res
def dfs(self,node,res):
if not node:
return
self.dfs(node.left,res)
self.dfs(node.right,res)
res.append(node.val)
leetcode 102 - Binary Tree Level Order Traversal [M] - stack or queue
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its level order traversal as:
[[3],
[9,20],
[15,7]]
leetcode 103 - Binary Tree Zigzag Level Order Traversal [M]
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its zigzag level order traversal as:
[[3],
[20,9],
[15,7]]
leetcode 107 - Binary Tree Level Order Traversal II (bottom-up) [E]
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its bottom-up level order traversal as:
[[15,7],
[9,20],
[3]]
from collections import deque
class BinaryTreeTraversal4():
#use queue
def levelorder_queue(self,root):
res=[]
if not root:
return res
q=deque()
q.append(root)
while q:
level=[]
for i in range(len(q)):
node=q.popleft()
level.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
res.append(level)
return res
#use stack
def levelorder_stack(self,root):
res=[]
if not root:
return res
q=[root]
#cnt=0
while q:
res.append([node.val for node in q])
#leetcode 103 zigzag
#if cnt%2==0:
# res.append([node.val for node in q])
#else:
# res.append([node.val for node in reversed(q)])
new_q=[]
for node in q:
if node.left:
new_q.append(node.left)
if node.right:
new_q.append(node.right)
q=new_q
#cnt+=1
return res
#leetcode 107
#return res[::-1]
leetcode 199 - Binary Tree Right Side View [M] - level order traversal
Given a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example:
Input: [1,2,3,null,5,null,4]
Output: [1, 3, 4]
1 <---
/ \
2 3 <---
\ \
5 4 <---
Solution: similar as 102, but record the right most values, here use stack
class Solution():
def rightSideView(self,root):
res=[]
if not root:
return res
q=[root]
while q:
res.append(q[-1].val)
new_q=[]
for node in q:
if node.left:
new_q.append(node.left)
if node.right:
new_q.append(node.right)
q=new_q
return res
Construction
leetcode 105 - Construct Binary Tree from Preorder and Inorder Traversal [M]
For example, given
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
Return the following binary tree:
3
/ \
9 20
/ \
15 7
class TreeConstruction():
def buildTree(self, preorder, inorder):
if not preorder or not inorder:
return None
root=TreeNode(preorder[0])
idx=inorder.index(preorder[0])
root.left=self.buildTree(preorder[1:idx+1],inorder[:idx])
root.right=self.buildTree(preorder[idx+1:],inorder[idx+1:])
return root
leetcode 106 - Construct Binary Tree from Inorder and Postorder Traversal [M]
For example, given
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]
Return the following binary tree:
3
/ \
9 20
/ \
15 7
class TreeConstruction():
def buildTree(self, inorder, postorder):
if not inorder or not postorder:
return None
root=TreeNode(postorder[-1])
idx=inorder.index(postorder[-1])
root.left=self.buildTree(inorder[:idx],postorder[:idx])
root.right=self.buildTree(inorder[idx+1:],postorder[idx:-1])
return root
Problems
Simple - Same, Symmetric, Invert, Univalue, Path, Path Sum, Ancestor
leetcode 100 - Same Tree [E] - [T/F]
class TreeSimple():
def isSameTree(self, p, q):
if not p and not q:
return True
if not p or not q:
return False
if p.val!=q.val:
return False
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
leetcode 101 - Symmetric Tree [E] - [T/F]
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3
class TreeSimple():
def isSymmetricTree(self, root):
if not root:
return True
return self.isSym(root.left,root.right)
def isSym(self,left,right):
if not left and not right:
return True
if not left or not right:
return False
if left.val!=right.val:
return False
return self.isSym(left.left,right.right) and self.isSym(left.right,right.left)
leetcode 226 - Invert Binary Tree [E]
Input:
4
/ \
2 7
/ \ / \
1 3 6 9
Output:
4
/ \
7 2
/ \ / \
3 1 9 6
Solution:
invert(4)
4.left=invert(2), 4.right=invert(7)
| return 2 | return 7
2.left=invert(6), 2.right=invert(9) 7.left=invert(1), 7.right=invert(3)
| return 6 | return 9 | return 1 | return 3
6.left=invert(N) return None
6.right=invert(N) return None
class Solution():
def invertTree(self,root):
if not root:
return None
root.left,root.right=self.invertTree(root.right),self.invertTree(root.left)
return root
leetcode 250 - Count Univalue Subtrees [E]
Given a binary tree,count the number of uni-value subtrees
A uni-value subtree means all nodes of the subtree have the same value
see leetcode ref
Input: root=[5,1,5,5,5,null,5]
5
/ \
1 5*
/ \ \
5* 5* 5*
Output: 4
class Solution():
def countUnivalueSubtrees(self,root):
self.cnt=0
self.isUni(root)
return self.cnt
def isUni(self,node):
if not node.left and not node.right:
self.cnt+=1
return True
is_uni=True
if node.left:
is_uni=self.isUni(node.left) and is_uni and node.left.val==node.val
if node.right:
is_uni=self.isUni(node.right) and is_uni and node.right.val=node.val
self.cnt+=is_uni
return is_uni
leetcode 257 - Binary Tree Paths [E]
Given a binary tree, return all root-to-leaf paths.
Note: A leaf is a node with no children.
Input:
1
/ \
2 3
\
5
Output: [“1->2->5”, “1->3”]
Explanation: All root-to-leaf paths are: 1->2->5, 1->3
Solution 1: recursion
class Solution():
def binaryTreePaths(self, root):
if not root:
return []
res=[]
self.dfs(root,res,''+str(root.val))
return res
def dfs(self,node,res,path):
if not node.left and not node.right:
res.append(path)
if node.left:
self.dfs(node.left,res,path+'->'+str(node.left.val))
if node.right:
self.dfs(node.right,res,path+'->'+str(node.right.val))
Solution 2: iteration
class Solution():
def binaryTreePaths(self, root):
if not root:
return []
stack=[]
res=[]
stack.append((root,str(root.val)))
while stack:
node,path=stack.pop()
if not node.left and not node.right:
res.append(path)
if node.left:
stack.append((node.left,path+'->'+str(node.left.val)))
if node.right:
stack.append((node.right,path+'->'+str(node.right.val)))
return res
leetcode 112 - Path Sum [E]
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
Note: A leaf is a node with no children.
Given the below binary tree and sum = 22,
5*
/ \
4* 8
/ / \
11* 13 4
/ \ \
7 2* 1
class TreeSimple():
def hasPathSum(self,root,sum):
if not root:
return False
sum-=root.val
if sum==0 and not root.left and not root.right:
return True
return self.hasPathSum(root.left,sum) or self.hasPathSum(root.right,sum)
leetcode 113 - Path Sum II [M]
Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
Return:
[[5,4,11,2],
[5,8,4,5]]
class TreeSimple():
def pathSum(self, root, sum):
res=[]
if not root:
return res
self.dfs(root,sum,res,[root.val])
return res
def dfs(self,root,target,res,path):
if not root:
return
if sum(path)==target and not root.left and not root.right:
res.append(path)
return
if root.left:
self.dfs(root.left,target,res,path+[root.left.val])
if root.right:
self.dfs(root.right,target,res,path+[root.right.val])
leetcode 236 - Lowest Common Ancestor of a Binary Tree [M] see bst #Ancestor
Example:
Input: Given root=[3,5,1,6,2,0,8,null,null,7,4], p=5, q=1
3
/ \
5 1
/ \ / \
6 2 0 8
/ \
7 4
Output: 3
Input: same tree, p=5, q=4
Output: 5
Note: All of the nodes’ values will be unique, and p and q are different and must exist in the tree
class Solution():
def lowestCommonAncestor(self,root,p,q):
if not root or q==root or p==root:
return root
left=self.lowestCommonAncestor(root.left,p,q)
right=self.lowestCommonAncestor(root.right,p,q)
if left and right:
return root
return left or right
Hard - Max Path Sum, Sum Root to Leaf Numbers
leetcode 124 - Binary Tree Maximum Path Sum [H] (similar leetcode 687, leetcode 543)
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3]
1
/ \
2 3
Output: 6
Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 *20
/ \
*15 *7
Output: 42
Solution:
*1
(6)/ \(3)
*2 *3
(4)/ \(4)
4 *4
- use a variable to remember the max sum (cur_max) so far
- child node returns its max(left,right)+node.val to its parent, because only one leaf connection can be validated
- minus values should be all removed
class TreeHard():
cur_max=float('-inf') #two ways to definite class variable
def maxPathSum(self,root):
#self.cur_max=float('-inf')
self.dfs(root)
return self.cur_max
def dfs(self,root):
if not root:
return 0
left=self.dfs(root.left)
right=self.dfs(root.right)
if left<0:
left=0
if right<0:
right=0
self.cur_max=max(left+right+root.val,self.cur_max)
return max(left,right)+root.val
leetcode 129 - Sum Root to Leaf Numbers [M]
Example1:
Input: [1,2,3]
1
/ \
2 3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
Example 2:
Input: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
Solution: take example 2
|dfs(<4>,0) |
| sum=0+4=4|
|dfs(<9>,4)| + |dfs(<0>,4)| = 986+40 = 1026
| sum=49| | sum=40|
|dfs(<5>,49)|+|dfs(<1>,49)| = 495+491 = 986
| sum=495| | sum=491|
class TreeHard():
def sumNumbers(self,root):
return self.dfs(root,0) # 0 is sum
def dfs(self,root,sum):
if not root:
return 0
sum=sum*10+root.val
if not root.left and not root.right:
return sum
return self.dfs(root.left,sum)+self.dfs(root.right,sum)
