ALgorithms 5 - dynamic programming
Triangle
leetcode 118 - Pascal’s Triangle [E]
leetcode 119 - Pascal’s Triangle II [E]
Input: 5
Output:
[[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]]
class Solution(object):
#leetcode 118
def generate(self, n):
if n==0:
return []
dp=[[1]]
for i in range(1,n):
temp=[]
for j in range(i-1):
temp.append(dp[i-1][j]+dp[i-1][j+1])
temp.insert(0,1)
temp.insert(len(temp),1)
dp.append(temp)
return dp
#leetcode 119
def getRow(self,r):
row=[1]
for i in range(r):
row=[1]+[row[j]+row[j+1] for j in range(len(row)-1)]+[1]
return row
leetcode 120 - Triangle [M]
Input:
[[2],
[3,4],
[6,5,7],
[4,1,8,3]]
Output: 11
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11)
Solution: dp bottom up
Initialization:
dp = [4,1,8,3] <- last layer
Transition:
i = 0,1,2 <- len of upperlayer
dp[i] = min(dp[i],dp[i+1]) + triangle[upperlayer][i]
class Solution(object):
def minSum(self, tri):
n=len(tri)
dp=tri[-1]
for l in range(n-2,-1,-1): #l=2,1,0
for j in range(l+1): #l=2,i=0,1,2 | l=1,i=0,1 | l=0,i=0
dp[j]=min(dp[j],dp[j+1])+tri[l][j]
return dp[0]
Find Numbers
leetcode 279 - Perfect Squares [M]
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.
Solution:
dp[i] - min numbers to form squares
dp initial: dp[0] = 0, dp[1] = 1, dp[n] rest = n
dp transit: dp[i]=min(dp[i],dp[i-j*j]+1), j from 1
n=13, 13-2*2=9, dp[13]=min(dp[13]+dp[9]+1)
i j dp[i]
2 1 dp[2]=min(dp[2],dp[2-1*1]+1)=dp[1]+1=2
3 1 dp[3]=min(dp[3],dp[3-1*1]+1)=dp[2]+1=3
4 1 dp[4]=min(dp[4],dp[4-1*1]+1)=dp[3]+1=4
2 dp[4]=min(dp[4],dp[4-2*2]+1)=min(4,dp[0]+1)=1
5 1 dp[5]=min(dp[5],dp[5-1*1]+1)=dp[4]+1=2
2 dp[5]=min(dp[5],dp[5-2*2]+1)=min(2,dp[1]+1)=2
6 1
2
...
9 1
2
3
10 1
2
3
...
class Solution(object):
def numSquares(self,n):
dp=[n]*(n+1)
dp[0]=0
dp[1]=1
for i in range(2,n+1):
j=1
while j*j<=i:
dp[i]=min(dp[i],dp[i-j*j]+1)
j+=1
return dp[-1]
Paint Colors
leetcode 256 - Paint House (3 colors) [E]
There are a row of n houses, each house can be painted with one
of the three colors: red, blue or green. The cost of painting
each house with a certain color is different. You have to paint
all the houses such that no two adjacent houses have the same color.
The cost of painting each house with a certain color is represented by a n x 3 cost matrix. For example, costs[0][0] is the cost of painting house 0 with color red; costs[1][2] is the cost of painting house 1 with color green, and so on… Find the minimum cost to paint all houses.
Note:
All costs are positive integers.
Input: [[17,2,17],[16,16,5],[14,3,19]]
Output: 10=2+5+3
Explanation:
r b g
[17, 2, 17] house 1
[16, 16, 5] house 2
[14, 3, 19] house 3
dp ini: cost matrix, i starts from 1
dp transition:
dp[i][0]+=min(dp[i-1][1],dp[i-1][2])
dp[i][1]+=min(dp[i-1][0],dp[i-1][2])
dp[i][2]+=min(dp[i-1][0],dp[i-1][1])
[17, 2, 17]
\ / \
/ \ \
[16+2*, 16+17, 5+2]
/
-----------
/ /
[14+7, 3+7, 19+18*]
class Solution():
def minCost(self,cost):
if not cost:
return 0
dp=cost
for i in range(1,len(cost)):
dp[i][0]+=min(dp[i-1][1],dp[i-1][2])
dp[i][1]+=min(dp[i-1][0],dp[i-1][2])
dp[i][2]+=min(dp[i-1][0],dp[i-1][1])
return min(dp[-1])
leetcode 265 - Paint House (k colors) [H]
There are a row of n houses, each house can be painted with one
of the k colors. The cost of painting
each house with a certain color is different. You have to paint
all the houses such that no two adjacent houses have the same color.
The cost of painting each house with a certain color is represented by a n x k cost matrix. For example, costs[0][0] is the cost of painting house 0 with color 0; costs[1][2] is the cost of painting house 1 with color 2, and so on… Find the minimum cost to paint all houses.
Input: [[1,5,3],[2,9,4]]
Output: 5
Explanation:
0 1 2 color
[1,5,3] house 0
^ ¥
[2,9,4] house 1
¥ ^
Solution 1: TO(nk^2)
class Solution():
def minCost(self,cost):
if not cost:
return 0
dp=cost
for i in range(1,len(cost)):
for k in range(len(cost[i])):
dp[i][k]+=self.getMin(cost,i-1,k)
return min(dp[-1])
def getMin(self,cost,i,k):
minn=max(cost[i])
for i,c in enumerate(cost[i]):
if i==k:
continue
minn=min(minn,c)
return minn
Solution 2: TO(nk)
- use a list min_c to record min and second min idx of each house
- add previous cost of non current idx min
dp transition: dp[i][k]+=dp[i-1][min_c[k==min_c[0]]]
k=0, if min_c[0,x], k==0, +dp[i-1][min_c[1]]
k=1, if min_c[0,x], k!=0, +dp[i-1][min_c[0]]
Details:
0 1 2 3 color k min_c dp ini:
[1, 8, 4, 9] house 0 [0,2] dp=cost
^ ^ dp transition:
[6, 0, 3, 1] house 1 [1,3] dp[i][k]+=dp[i-1][min_c[k==min_c[0]]]
^ ^
[3, 7, 5, 4] house 2 [0,3]
^ ^
[2, 1, 9, 3] house 3 [1,0]
^ ^
[5, 0, 4, 7] house 4 [1,2]
^ ^
class Solution():
def minCost(self,cost):
if not cost or not cost[0]:
return 0
for i in range(1,len(cost)):
min_c=[0,1] #min and second min color idx
if cost[i-1][0]>cost[i-1][1]:
min_c=[1,0]
for c in range(2,len(cost[0])):
if cost[i-1][c]<=cost[i-1][min_c[0]]:
min_c[1],min_c[0]=min_c[0],c
elif cost[i-1][c]<cost[i-1][min_c[1]]:
min_c[1]=c
print(min_c)
for c in range(len(cost[0])):
cost[i][c]+=cost[i-1][min_c[c==min_c[0]]]
return min(cost[-1])
leetcode 276 - Paint Fence [E]
There is a fence with n posts, each post can be painted with one of the k colors.
You have to paint all the posts such that no more than two adjacent fence posts have the same color.
Return the total number of ways you can paint the fence.
Input: n=3,k=2
Output: 6
post1 post2 post3
1 c1 c1 c2
2 c1 c2 c1
3 c1 c2 c2
4 c2 c1 c1
5 c2 c1 c2
6 c2 c2 c1
Solution:
n possibility(colors)
1 k
2 k*1+k*(k-1) same: k*1, diff: k*(k-1)
3 k*(k-1)+k*(k-1)\*(k-1) same: k*(k-1) - 1,2same:k, 3:k-1 or 1:k, 2,3same:k-1
diff: k*(k-1)\*(k-1)
class Solution():
def numWays(self,n,k):
if k==0 or n==0:
return 0
if n==1:
return k
same=k
diff=k*(k-1)
for i in range(3,n+1):
same,diff=diff,(same+diff)*(k-1)
return same+diff
String Subsequence
leetcode 115 - Distinct Subsequences [H]

note: subsequence can jump some char but should be in order
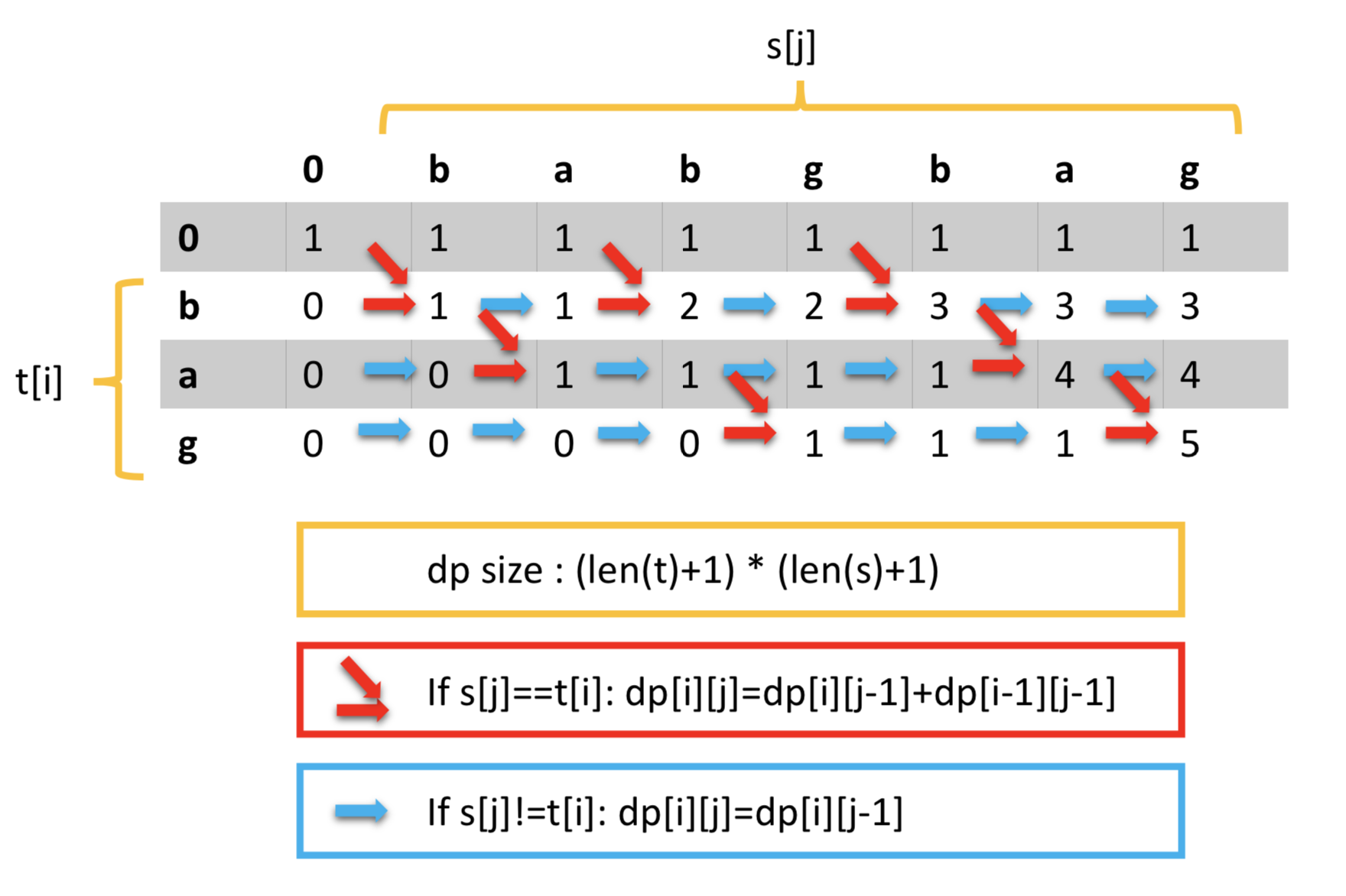
class Solution(object):
def numDistinct(self, s, t):
dp=[[0 for j in range(len(s)+1)] for i in range(len(t)+1)]
for j in range(len(s)+1):
dp[0][j]=1
for i in range(1,len(t)+1):
for j in range(1,len(s)+1):
if t[i-1]==s[j-1]:
dp[i][j]=dp[i][j-1]+dp[i-1][j-1]
else:
dp[i][j]=dp[i][j-1]
return dp[-1][-1]
Word Break
leetcode 139 - Word Break [M]
Example 1:
Input: s = “leetcode”, wordDict = [“leet”, “code”]
Output: true
Explanation: Return true because “leetcode” can be segmented as “leet code”.
Example 2:
Input: s = “applepenapple”, wordDict = [“apple”, “pen”]
Output: true
Explanation: Return true because “applepenapple” can be segmented as “apple pen apple”.
Note that you are allowed to reuse a dictionary word.
Example 3:
Input: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
Output: false
Example 1 Solution:
Initialization:
dp=[T,F,F,F,F,…] (len=len(s)+1)
i is for s[:i]
l e e t c o d e
0 1 2 3 4 5 6 7 8
initial T F F F F F F F F
i=4 k=0 T F F F T F F F F
i=8 k=4 T F F F T F F F T
i=1 k=0 dp[0]=T, s[0:1] not in Dict
i=2 k=0 dp[0]=T, s[0:2] not in Dict
k=1 dp[1]=F, s[1:2] not in Dict
i=3 k=0 dp[0]=T, s[0:3] not in Dict
k=1 dp[1]=F, s[1:3] not in Dict
k=2 dp[2]=F, s[2:3] not in Dict
i=4 k=0 dp[0]=T, s[0:4] 'leet' in Dict -> dp[4]=T
...
i=8 k=4 dp[4]=T, s[4:8] 'code' in Dict -> dp[8]=T
...
class Solution(object):
def wordBreak(self, s, wordDict):
dp=[False]*(len(s)+1)
dp[0]=True
for i in range(1,len(s)+1):
for k in range(i):
if dp[k] and s[k:i] in wordDict:
dp[i]=True
return dp.pop()
leetcode 140 - Word Break II [H] - dp + dfs
Example 2:
Input:
s = “pineapplepenapple”
wordDict = [“apple”, “pen”, “applepen”, “pine”, “pineapple”]
Output:
[ “pine apple pen apple”,
“pine applepen apple”,
“pineapple pen apple”]
Explanation: Note that you are allowed to reuse a dictionary word.
Example 2 Solution:
-
check if s can be broken into dict words
|dfs('pineapplepenapple',dict,'',res) |#s[:4]='pine' in dict |dfs('applepenapple',dict,'pine ',res) |~s[:5]='apple' in dict |dfs('penapple',dict,'pine apple ',res) |s[:3]='pen' in dict |dfs('apple',dict,'pine apple pen ',res) |s[:5]='apple' in dict |dfs('',dict,'pine apple pen apple',res) <- append res |~s[:8]='applepen' in dict |dfs('apple',dict,'pine applepen ',res) |s[:5]='apple' in dict |dfs('',dict,'pine applepen apple',res) <- append res |#s[:9]='pineapple' in dict |dfs('penapple',dict,'pineapple ',res) |s[:3]='pen' in dict |dfs('apple',dict,'pineapple pen ',res) |s[:5]='apple' in dict |dfs('',dict,'pineapple pen apple',res) <- append res
class Solution():
def wordBreak(self, s, wordDict):
res = []
self.dfs(s, wordDict, '', res)
return res
def check(self, s, dict):
dp = [False for i in range(len(s)+1)]
dp[0] = True
for i in range(1, len(s)+1):
for k in range(i):
if dp[k] and s[k:i] in dict:
dp[i] = True
return dp.pop()
def dfs(self, s, dict, stringlist, res):
if self.check(s, dict):
if not s:
res.append(stringlist[1:])
for i in range(1, len(s)+1):
if s[:i] in dict:
self.dfs(s[i:], dict, stringlist+' '+s[:i])
Matrix Region Search
leetcode 221 - Maximal Square [M] - dp Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
Example:
Input:
1 0 1 0 0
1 0 1* 1* 1
1 1 1* 1* 1
1 0 0 1 0
Output: 4
Solution:
dp[i][j] is the length of constructable rectangle, as the lower right point
dp initial, start from dp[1][1]
1 0 1 0 0
1 s
1
1
dp transit
dp[i][j]=min(dp[i-1][j-1]+dp[i-1][j]+dp[i][j-1])+1
class Solution():
def maximalSquare(self,matrix):
if not matrix:
return 0
row,col=len(matrix),len(matrix[0])
dp=[[1 if matrix[i][j]=='1' else 0 for j in range(col)] for i in range(row)]
for i in range(1,row):
for j in range(1,col):
if matrix[i][j]=='1':
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1
else:
dp[i][j]=0
res=[i for sub in dp for i in sub]
return max(res)**2
