Soft Q-Learning
Background
keywords:
- energy-based policies <- boltzmann distribution
- max-entropy policies
- amortized stein variational gradient descent
DRL:
a promising direction for autonomous acquisition of complex behaviors
(+) can process complex sensory input
(+) so that can acquire elaborate behavior skills using general-purpose neural network representations
However,
(-) most DRL methods operate on the conventional deterministic notion of optimality, where the optimal solution, at least under full observability, is always a deterministic policy
Stochastic policies are desirable for exploration, usually heuristically:
- by injecting noise
- by initializing a stochastic policy with high entropy
Sometime stochastic behaviors are required, the reasons are:
- exploration in the presence of multimodel objectives
- compositionality attained via pretraining
Other benefits:
- robustness in the face of uncertain dynamics
- imitation learning
- improved convergence and computational properties
- multi-modality application
Goal:
must define an objective that promotes stochasticity
A stochastic policy emerges as the optimal answer when we consider the connection between optimal control and probabilistic inference. [2]
Framing control as inference produces policies that aim to capture
- the single deterministic behavior that has the lowest cost
- the entire range of low-cost behaviors, explicitly maximizing the entropy of the corresponding policy
Instead of learning the best way to perform the task, the resulting policies try to learn all of the ways of performing the task.
The resulting policy can serve as:
(+) a good initialization for finetuning to a more specific behavior (learn separate running and bounding skills)
(+) a better exploration mechanism for seeking out the best mode in a multimodel reward landscape
(+) a more robust behavior in the face of adversarial perturbations
Related methods for solving such maximum entropy stochastic policy learning problems:
- Z-learning
- max-entropy inverse RL
- approximate inference using message passing
- Ψ-learning
- G-learning
- PGQ (Combining policy gradient and Q-learning)
Problems of the related methods:
(-) operate on simple tabular representations
(-) employ a simple parametric representation of the policy distribution auch as a conditional Gaussian
Therefore, the resulting distribution is limited in terms of its representational power even if the parameters of the distribution are represented by an expressive function approximator such as neural network
The question:
How can we extend the framework of max-entropy policy search to arbitrary policy distributions?
Solution:
- energy-based models (EBM)
which can reveal connections between Q-learning, actor-critic and probabilistic inference
The proposed methods:
- formulate a stochastic policy as a EBM, with the energy function corresponding to the “soft” Q-function obtained when optimizing the max-entropy objective
difficulty:
(-) in high dimensional continuous spaces, sampling from the EBM policy is intractable
- devise an approximate sampling procedure based on training a separate sampling network, which is optimized to produce unbiased samples from the policy EBM
- the sampling network can then be used both for updating the EBM and for action selection
in actor-critic, actor <- the sampling network
=> entropy regularized actor-critic can be viewed as approximate Q-learning, with the actor serving the role of an approximate sampler from an intractable posterior
Related methods:
- deterministic policy gradient (DPG)
- normalized advantage functions (NAF)
- policy gradient Q-learning (PGQ)
Contributions:
- a tractable efficient algorithm for optimizing arbitrary multimodal stochastic policies represented by energy-based models
- a discussion that relates this method to others in RL and probabilistic inference
Experiment results:
- show improved exploration performance in tasks with multi-model reward landscapes
- a degree of compositionality in RL, by showing that stochastic energy-based policies can serve as a much better initialization for learning new skills
Context
MaxEnt RL problem formulation

Note that, the MaxEnt objective differs qualitatively from
- Boltzmann Exploration
- PGQ
BE and PGQ greedily maximize entropy at the current time step, but do not explicitly optimize for policies that aim to reach states where they will have high entropy in their future
While the MaxEnt objective can maximize the entropy of the entire traj distribution for the policy pi
Policy Representation
prior work:
- discrete multinomial distributions
- Gaussian distributions
However, engergy-based model is more general class of distribution that can represent complex, multimodal behaviors
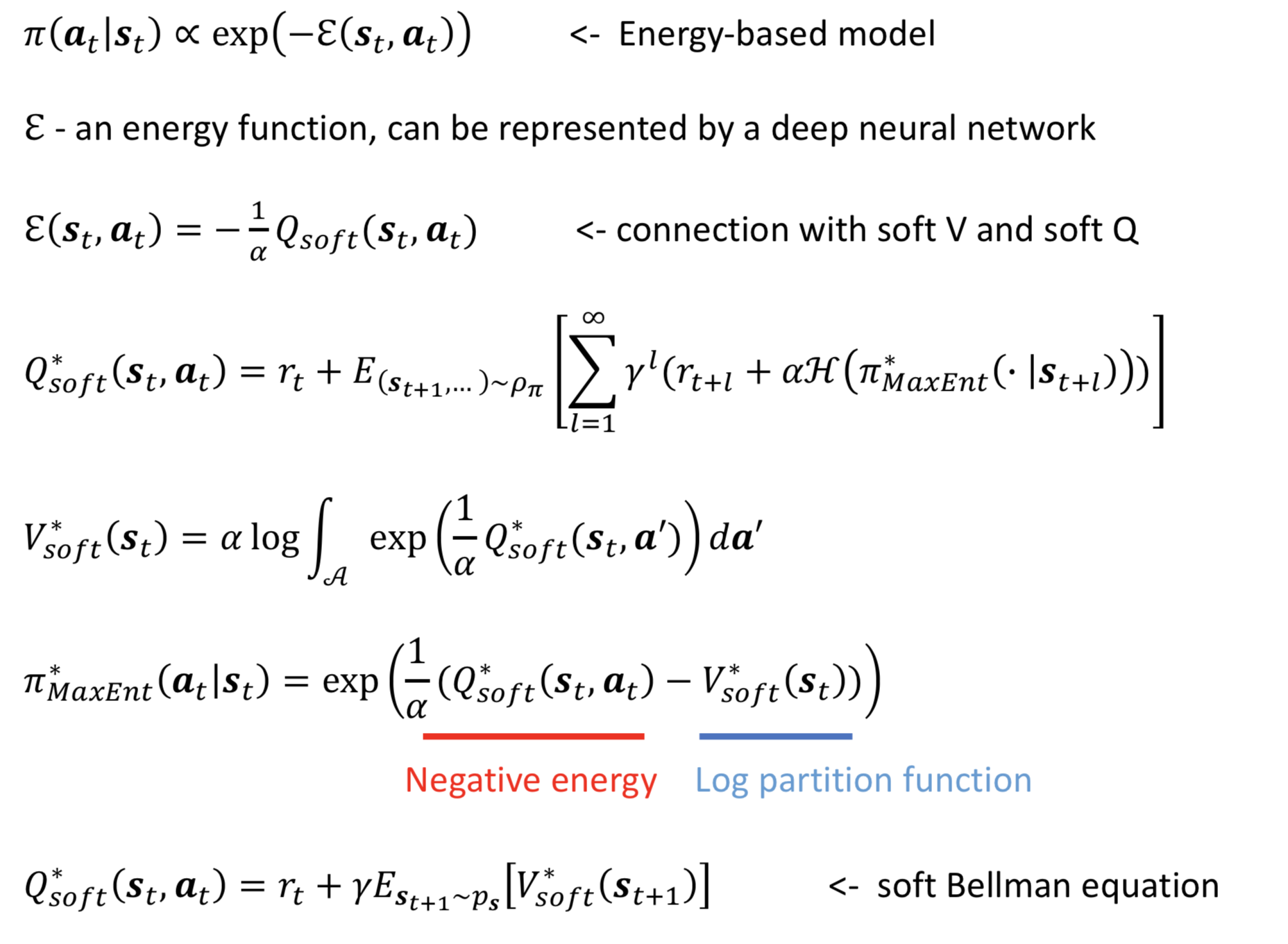
Soft Q-Learning
Soft Q-Iteration

Practical Problems
- the soft Bellman backup cannot be performed exactly in continuous or large state and action spaces
- sampling from the energy-based model is intractable in general
Soft Q-Learning
Normally, since the soft Bellman backup is a contraction, the optimal value function is the fixed point of the Bellman backup
We can find Q* by minimizing the soft Bellman error |𝒯Q-Q|, where 𝒯 is the soft bellman operator
However, This procedure is intractable due to the integral in V_soft(st)
Solution:
Turn this procedure into a stochastic optimization, which leads to a SGD update

This SGD can be updated using sampled states and actions, the sampling distribution qs and qa can be arbitrary
We can use real samples from rollouts of current policy π(at|st) ∝ exp[1/α(Q_soft^θ(st,at))]
For qa’, can be uniform, or can be the current policy which produces an unbiased estimate of the soft value as can be confirmed by substitution
(-) uniform scale poorly to high dimensions
Problem:
In continuous spaces, we still need a tractable way to sample from the policy π(at|st) ∝ exp[1/α(Q_soft^θ(st,at))], both to take on-policy actions and to generate action samples for estimating the soft value function
Since the form of the policy is so general, sampling from it is intractable
Solution:
will need to use an approximate sampling procedure
Approximate Sampling
How to sample from the soft Q-function?
Two categories of sampling from energy-based distribution:
- Markov chain Monte Carlo (MCMC) [Sallans & Hinton, 2004]
- learn a stochastic sampling network trained to output approximate samples from the target distribution [Zhao et al, 2016] [Kim & Bengio, 2016]
MCMC:
(-) MCMC is not tractable when the inference must be performed online (i.e. when excuting a policy)
Use:
- SVGD - a sampling network based on Stein Variational Gradient Descent [Liu & Wang, 2016]
- amortized SVGD [Wang & Liu, 2016]
amortized SVGD properties:
- provides with a stochastic sampling network that we can query for extremely fast sample generation
- be shown to converge to an accurate estimate of the posterior distribution of an EBM
- the resulting algorithm strongly resembles actor-critic, which provides for a simple and computationally efficient implementation
Formally, we want to learn a state-conditioned stochastic neural network:

Algorithm Summary
propose: the soft Q-learning algorithm for learning maximum entropy policies in continuous domains
- collecting experience
- updating soft Q function and sampling networks
parameters are updated using random mini-batch from the memory D (same as DQN)
soft Q function updates use a delayed version of the target values (same as DQN)
Algorithm 1: Soft Q-learning:
θ - Qsoft network parameters
𝜙 - sampling network parameters
initialize θ,𝜙
set up target value for θ|,𝜙|
set up memory D
for each episode:
for each time step:
collect experience {s,a,s',r}
a <- f^𝜙(ξ;s), where ξ~N(0,1) <- sample an action for s using f^𝜙
s' <- p(s'|s,a) <- sample next state from the env
D <- D ∪ {s,a,s',r} <- save the new experience in the memory
{(s,a,s',r)^i}^N ~ D <- sample a mini batch from the memory, i.e. N=32, i=0~N
[Update Soft Q]
sample {a_i,j}^M ~ q_a' for each s'^i <- q_a' from importance sampling j=0~M
compute empirical Vsoft^θ|(s'^i)
compute empirical gradient ∇θ JQ
update θ according to ∇θ JQ using ADAM
[update policy]
sample {ξ_i,j}^M ~ N(0,1) for each s^i
compute action a_i,j=f^𝜙(ξ_i,j;s)
compute ∆f^𝜙 using empirical estimate
compute empirical estimate of ∇𝜙 Jπ
update 𝜙 according to ∇𝜙 Jπ using ADAM
update target parameter θ|,𝜙| every fixed period
Experiment
Didactic Task of Multi-Goal Env:
| G |
| |
| |
------- | | -------
G S G
------- | | -------
| |
| |
| G |
Other tasks with multi-modality:
- a chess player might try various strategies before settling on one that seems most effective
- an agent navigating a maze may need to try various paths before finding the exit
During the learning process, it is often best to keep trying multiple available options until the agent is confident that one of them is the best. (similar to a bandit problem)
However, DRL for continuous control typically use unimodal action distributions which are not well suited to capture sum multi-modality.
So they may prematurely commit to one mode and converge to suboptimal behavior.
To evaluate how maximum entropy policies might aid exploration, conduct two experiments:
- a simulated swimming snake - it receives a reward euqal to its speed along the x-axis, either forward or backward. Once the swimmer swims far enough forward, it crosses a “finish line” and receives a larger reward
- a quadrupedal 3D robot needs to find a path through a maze to a target position - a more complex task with a continuous range of equally good options prior to discovery of a sparse reward goal
Pre-trained MaxEnt Policies
Task-specific initialization: [Goodfellow et al, 2016] <- a standard way to accelerate DNN
a network trained for one task is used as initialization for another task
First task can be highly general, i.e. classifying a large image dataset
Second task can be more specific, i.e. fine-grained classification with a small dataset
However, in RL, near-optimal policies are often near-deterministic, which makes them poor initializers foe new tasks.
Discrete Soft QL
based on [8]
Motivation:
- complex RL tasks sometimes require longer training, transferring and relearning
Soft QL:
(+) focuses on policy composability, that complex task can be decomposed to several simpler tasks for efficiency improvement
(+) With the rearrangement of the learned policies, more emerging complex tasks can be relearned
(-) Since Soft QL was working on continuous action spaces, it can obtain smooth behavior, however, analytical solution was difficult to obtain with the integral term
(-) sampling of the behavior is also difficult, that it’s not applicable on real robot learning
So discrete action space can be reconsidered for versatile learning
Max-Ent RL:
Classic RL assumes static environment, and obtains the optimal policies by policy iteration.
However, when the environment varies, the optimal policies needs to be adaptive as well.
∞
π* (at|st) = argmax E [ Σ γ^t R | s0=s ]
π π(a|s) t=0
T(s'|s,a)
∞
π* (at|st) = argmax E [ Σ γ^t R + αEnt H(π(.|st)) | s0=s ]
MaxEnt π π(a|s) t=0
T(s'|s,a)
∞
H(p(.)) = - ∫ p(i)logp(i) di
-∞
αEnt - parameter for trade of max-ent policy and normal max-expected-return learning
Max-Ent RL learns by maximizing expected return, at the same time, maximizing the entropy term H as well.
Suppose a grid world task:
|---------------------| |----------------|----|
| -------------> G | | -----------X | G |
| | | | | | ^ |
| Agt ------------ | | Agt -----------| | |
| | | | | |
| | | |----------------| |
|---------------------| |---------------------|
before env changed after env changed
Classic RL finds the optimal policy that is the path with the minimal step lengths towards the goal as the left fig.
However, once the environment changed by adding a wall on the upper route shown as the right fig, following the shortest path cannot lead the agent to the goal anymore.
In this case, Max-Ent RL is looking for not only the shortest path, but for other possible paths with various behaviors. When the environment changes, it can adapt to the change quickly.
When the entropy of a probability gets large, it’s close to uniform distribution.
When the entropy of a policy gets large, more various behaviors can be obtained.
Composable DRL for Robotic Manipulation
Soft QL:
(+) soft QL can learn multi-model exploration strategies by learning policies represented by expressive energy-based models
(+) policies learned with soft QL can be composed to create new policies and the optimality of the resulting policy can be bounded in terms of the divergence between the composed policies
Applying model-free DRL to real-world robotic control problems is difficult:
(-) the sample complexity of model-free methods tends to be high, and is increased further by the inclusion of high-capacity function approximators
MaxEnt policies:
-
provide an inherent, informed exploration strategy by expressing a stochastic policy via the Boltzmann distribution with the energy corresponding to the reward-to-go or Q-function
This policy distribution assigns a non-zero probability to all actions, but actions with higher expected rewards are more likely to be sampled
As a result, the policy will automatically direct exploration into regions of higher expected return -
independently trained MaxEnt policies can be composed together by adding their Q-functions, yielding a new policy for the combined reward function that is provably close to the corresponding optimal policy
Refs
[1] Haarnoja, T., Tang, H., Abbeel, P. and Levine, S., 2017, August. Reinforcement learning with deep energy-based policies. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (pp. 1352-1361). JMLR. org.
[8] 迷路探索問題に対するSoft Q-learningの適用と方策合成性の検証
[9] Haarnoja, T et al. Composable Deep Reinforcement Learning for Robotic Manipulation
Control and Inference
[2] Todorov, E. General duality between optimal control and estimation. In IEEE Conf. on Decision and Control, pp. 4286–4292. IEEE, 2008.
[3] Toussaint, M. Robot trajectory optimization using approximate inference. In Int. Conf. on Machine Learning, pp. 1049–1056. ACM, 2009.
Boltzmann Exploration
[4] Sallans, B. and Hinton, G. E. Reinforcement learning with factored states and actions. Journal of Machine Learning Research, 5(Aug):1063–1088, 2004.
Policy Gradient and Q-learning
[5] O’Donoghue, B., Munos, R., Kavukcuoglu, K., and Mnih, V. PGQ: Combining policy gradient and Q-learning. arXiv preprint arXiv:1611.01626, 2016.
Soft V and Q
[6] Ziebart, B. D. Modeling purposeful adaptive behavior with the principle of maximum causal entropy. PhD thesis, 2010.
[7] Fox, R., Pakman, A., and Tishby, N. Taming the noise in reinforcement learning via soft updates. In Conf. on Uncertainty in Artificial Intelligence, 2016.
