Jiexin Wang

Reinforcement Learning
Mobile & Joint Robots

Background

Stochastic optimization (SO) methods are optimization methods for minimizing or maximizing an objective function when randomness is present.

Randomness Injection through:

  • the objective functions
  • the constraint sets

can be other ways like random iterates, etc

Algorithms

  • stochastic approximation SA [Robbins and Monro 1951]
  • stochastic gradient descent
  • finite-difference SA [Kiefer and Wolfowitz 1952]
  • simultaneous perturbation SA [Spall 1992]
  • scenario optimization

Example Problem

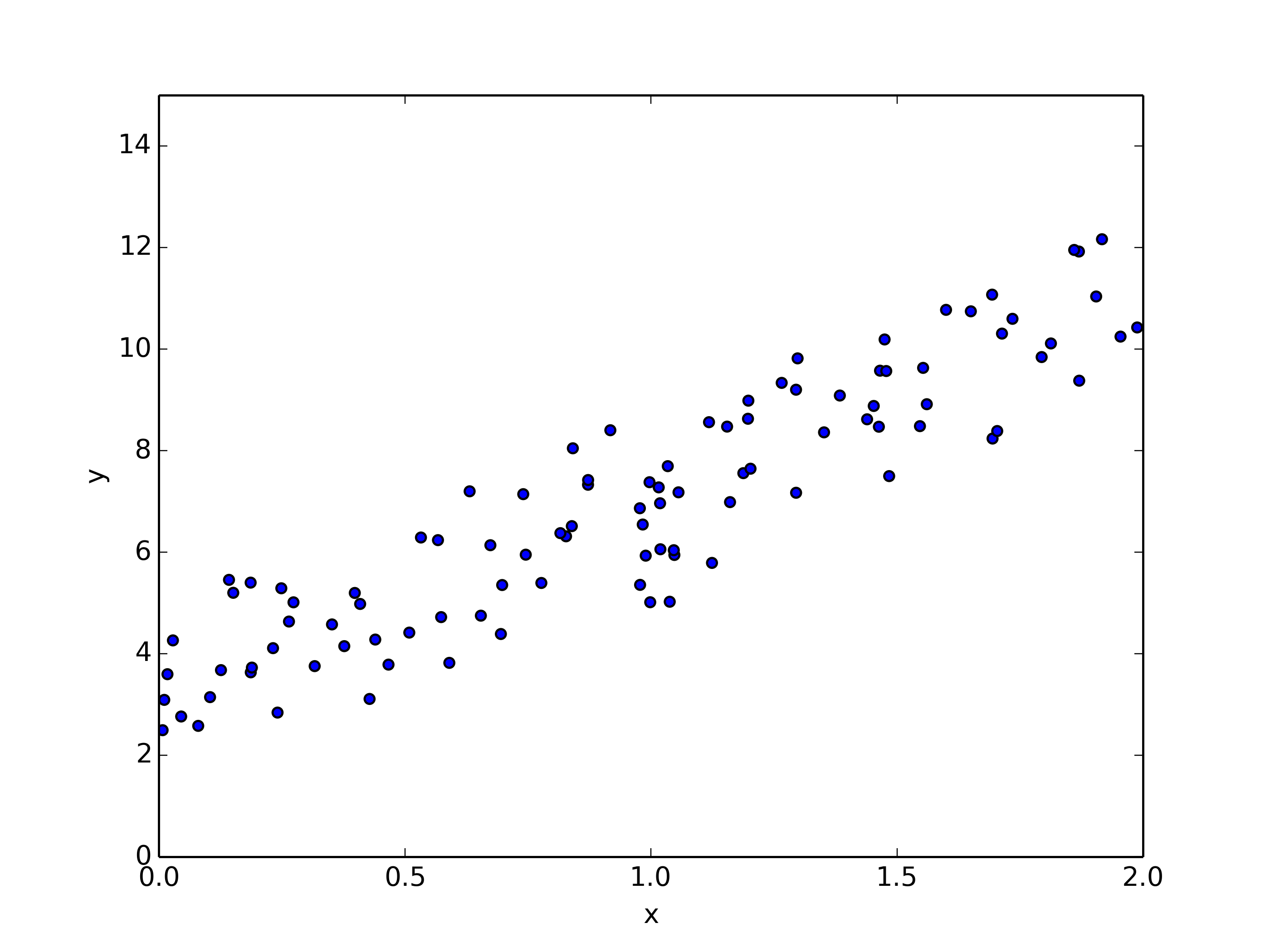
Given data generated from y=ax+b+ε, a=4, b=3: y=4x+3+ε find its estimated line

import numpy as np

x=2*np.random.rand(100)  #0~2 uniform distribution data
y=3+4*x+np.random.randn(100)  #0~1 normal distribution noise

Analytical Solution

import matplotlib.pyplot as plt

n=len(x)
no=x.dot(y)-n*np.mean(x)*np.mean(y)  #nominator
de=np.sum(np.power(x,2))-n*(np.mean(x))**2  #denominator
a_hat=no/de  #4.117081503484073
b_hat=np.mean(y)-a_hat*np.mean(x)  #2.936328604388291

y_hat=a_hat*x+b_hat

plt.scatter(x,y)
plt.plot(x,y_hat,'r')

numpy.linalg.lstsq

X=np.vstack([x,np.ones(len(x))]).T    
a,b=np.linalg.lstsq(X, y, rcond=None)[0]

numpy.linalg.inv - regression in matrix

X = 2 * np.random.rand(100,1)
y = 4 +3 * X+np.random.randn(100,1)
X_b = np.c_[np.ones((100,1)),X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

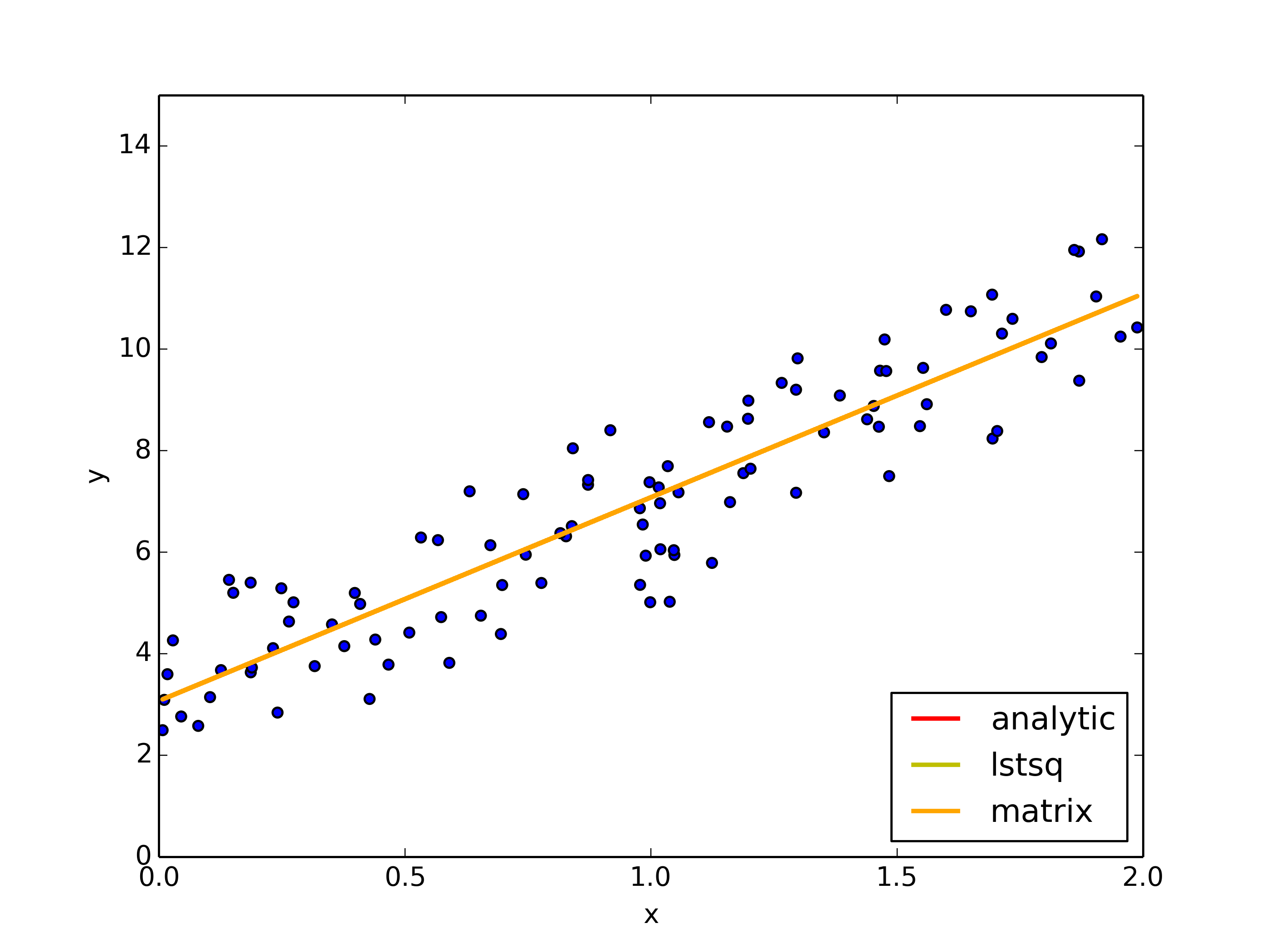
Problem:
If the #feature increases, it’s hard to do the matrix multiplication anymore.

Solution:

Gradient Descent

Like descending down a mountain without assistance but information about the height over sea-level.
Repeatedly choose a direction and check if the height is smaller than before.

Machine learning analogy:

  • learning rate - size of per step
  • objective function - height
  • gradient - direction of each step

Reformulate the problem setting:

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt

x=2*np.random.rand(100,1)  #0~2 uniform distribution data
y=3+4*x+np.random.randn(100,1)  #0~1 normal distribution noise

def objective(theta,x,y):
    n=len(y)
    pred=x.dot(theta)
    obj=(1/2*n)*np.sum(np.square(pred-y))

    return obj

def gradient_descent(x,y,theta,alpha=0.01,iter=1000):

    #data size
    #x - 100x1, X - 100x2
    #y - 100x1, pred - 100x1 - X*theta=100x2x2x1
    #theta - 2x1
    #grad - 2x1 - xT*(pred-y)=2x100x100x1
    #theta_traj - 100x2
    #grad_traj - 100x2
    #obj_traj - 100

    n=len(y)
    obj_traj=np.zeros(iter)
    theta_traj=np.zeros((iter,2))

    for i in range(iter):
        pred=x.dot(theta)
        grad=(1/n)*(x.T.dot((pred-y)))
        theta=theta-alpha*grad

        theta_traj[i,:]=theta.T
        obj_traj[i]=objective(theta,x,y)

    return theta, theta_traj, obj_traj

#initilization
alpha=0.01
n_iter=1000
theta=np.random.randn(2,1)
X=np.c_[np.ones((len(x),1)),x] #[[1,x0],[1,x1]...

theta,theta_traj,obj_traj=gradient_descent(X,y,theta,alpha,n_iter)

plt.scatter(x,y,label='origin')
plt.plot(x,theta[1]*x+theta[0],'g',label='gradient_descent')

Fitted results and the parameter trajs

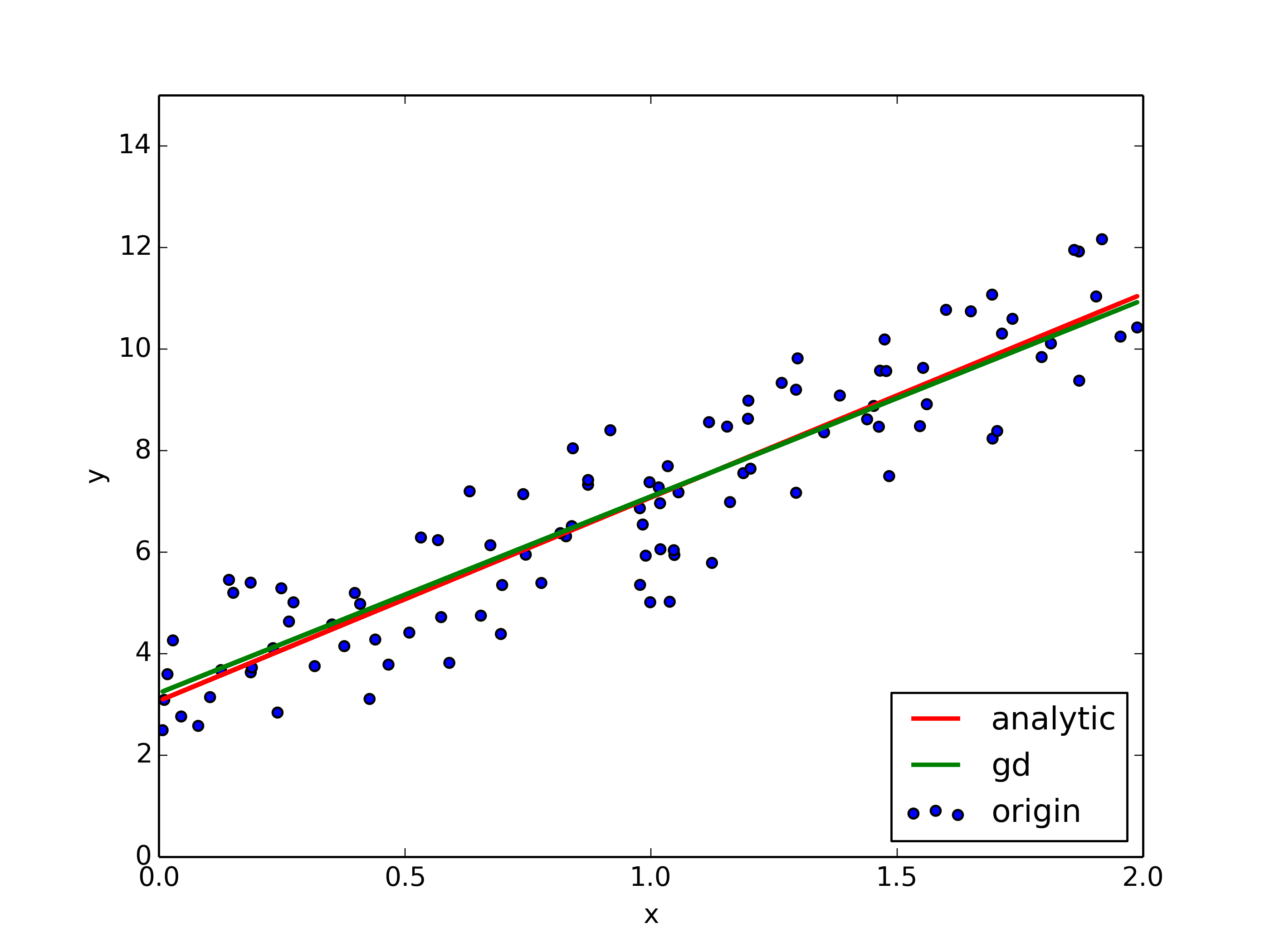
Stochastic Gradient Descent

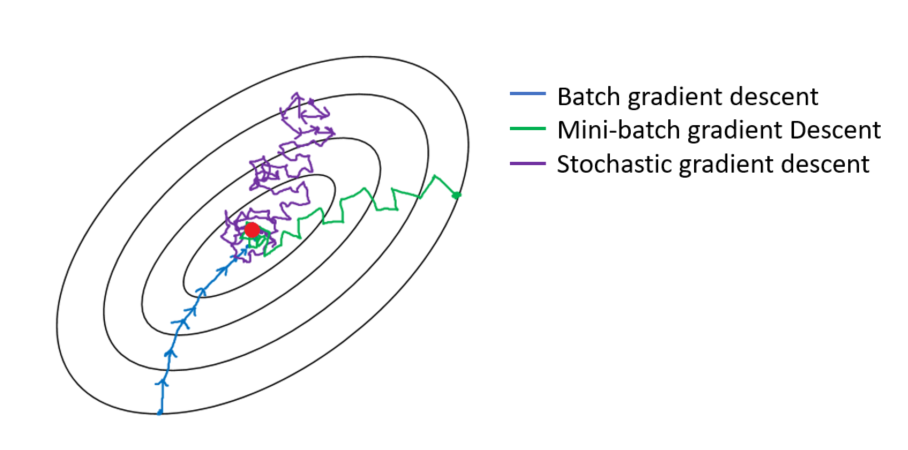
In Gradient Descent, parameter gradients are computed on all observations (sample) at each iteration.
In Stochastic Gradient Descent, we can choose the observation (sample) randomly instead of a single group or in the order they appear in the training set.

def sgd(x,y,theta,alpha=0.01,iter=1000):

    #data size
    #X - 100x2
    #y - 100x1,
    #x_i - 1x2
    #y_i - 1x1
    #theta - 2x1
    #pred - 1x1 - x_i*theta=1x2x2x1
    #grad - 2x1 - x_iT*(pred-y)=2x1x1x1
    #theta_traj - 100x2
    #grad_traj - 100x2
    #obj_traj - 100

    n=len(y)
    obj_traj=np.zeros(iter)
    grad_traj=np.zeros((iter,2))

    for i in range(iter):
        obj=0
        for j in range(n):
            rand_i=np.random.randint(0,n)
            x_i=x[rand_i,:].reshape(1,x.shape[1])
            y_i=y[rand_i].reshape(1,1)
            pred=x_i.dot(theta)
            grad=(1/n)*(x_i.T.dot((pred-y_i)))
            theta=theta-alpha*grad
            obj+=objective(theta,x_i,y_i)

        grad_traj[i,:]=grad.T
        obj_traj[i]=obj

    return theta, obj_traj, grad_traj

#initilization
alpha=0.01
n_iter=1000
theta=np.random.randn(2,1)
X=np.c_[np.ones((len(x),1)),x]
theta,obj_traj,grad_traj=sgd(X,y,theta,alpha,n_iter)

Mini-Batch Stochastic Gradient Descent

Uses random samples in batches.

def mini_sgd(x,y,theta,alpha=0.01,iter=1000,batch_size=20):

    #data size
    #X - 100x2
    #y - 100x1,
    #batch size 20
    #x_i - 20x2
    #y_i - 20x1
    #theta - 2x1
    #pred - 20x1 - x_i*theta=20x2x2x1
    #grad - 2x1 - x_iT*(pred-y)=2x20x20x1
    #theta_traj - 100x2
    #grad_traj - 100x2
    #obj_traj - 100

    n=len(y)
    obj_traj=np.zeros(iter)
    grad_traj=np.zeros((iter,2))

    for i in range(iter):
        obj=0
        i_s=np.random.permutation(n)
        x=x[i_s]
        y=y[i_s]
        for j in range(0,n,batch_size):  #[0,20,40,60,80]
            x_i=x[j:j+batch_size]
            y_i=y[j:j+batch_size]
            pred=x_i.dot(theta)
            grad=(1/n)*(x_i.T.dot((pred-y_i)))
            theta=theta-alpha*grad
            obj+=objective(theta,x_i,y_i)

        obj_traj[i]=obj
        grad_traj[i,:]=grad.T

    return theta, obj_traj, grad_traj

#initilization
alpha=0.01
n_iter=1000
#alpha_m=0.1
#n_iter_m=200
theta=np.random.randn(2,1)
batch_size=20
X=np.c_[np.ones((len(x),1)),x]
theta_msgd,obj_traj_msgd,grad_traj_msgd=mini_sgd(X,y,theta,alpha,n_iter,batch_size)

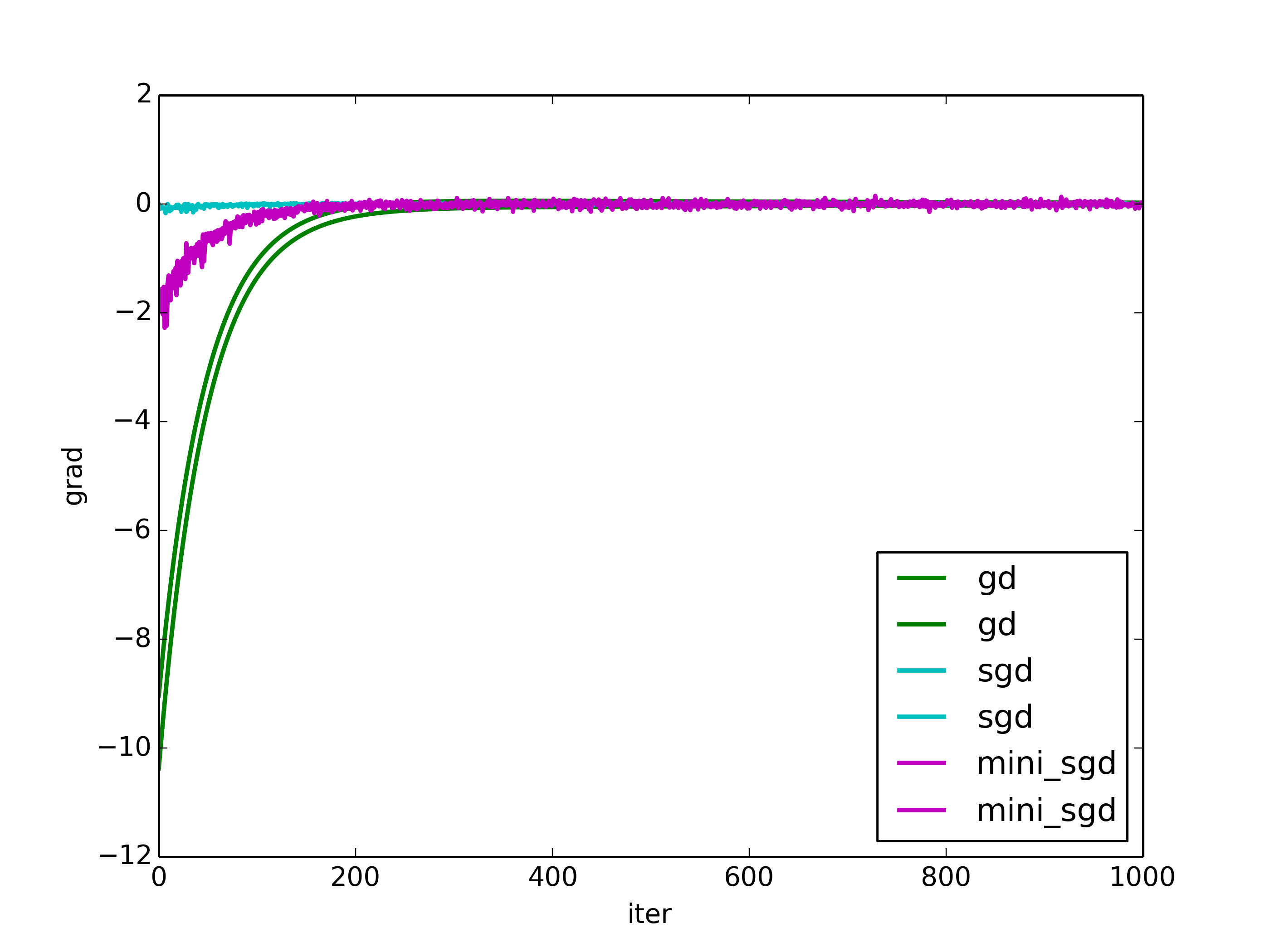
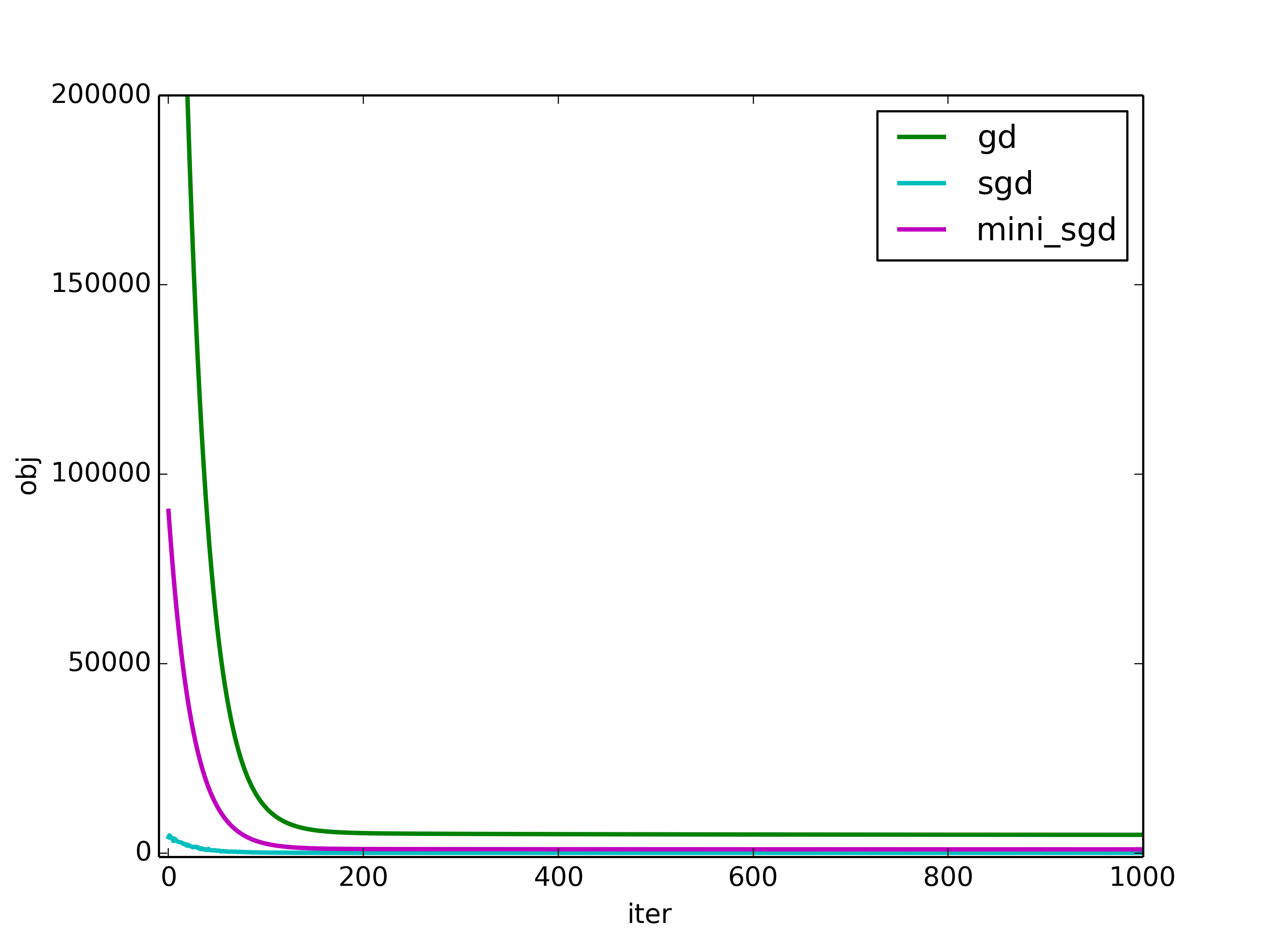
Fitted results

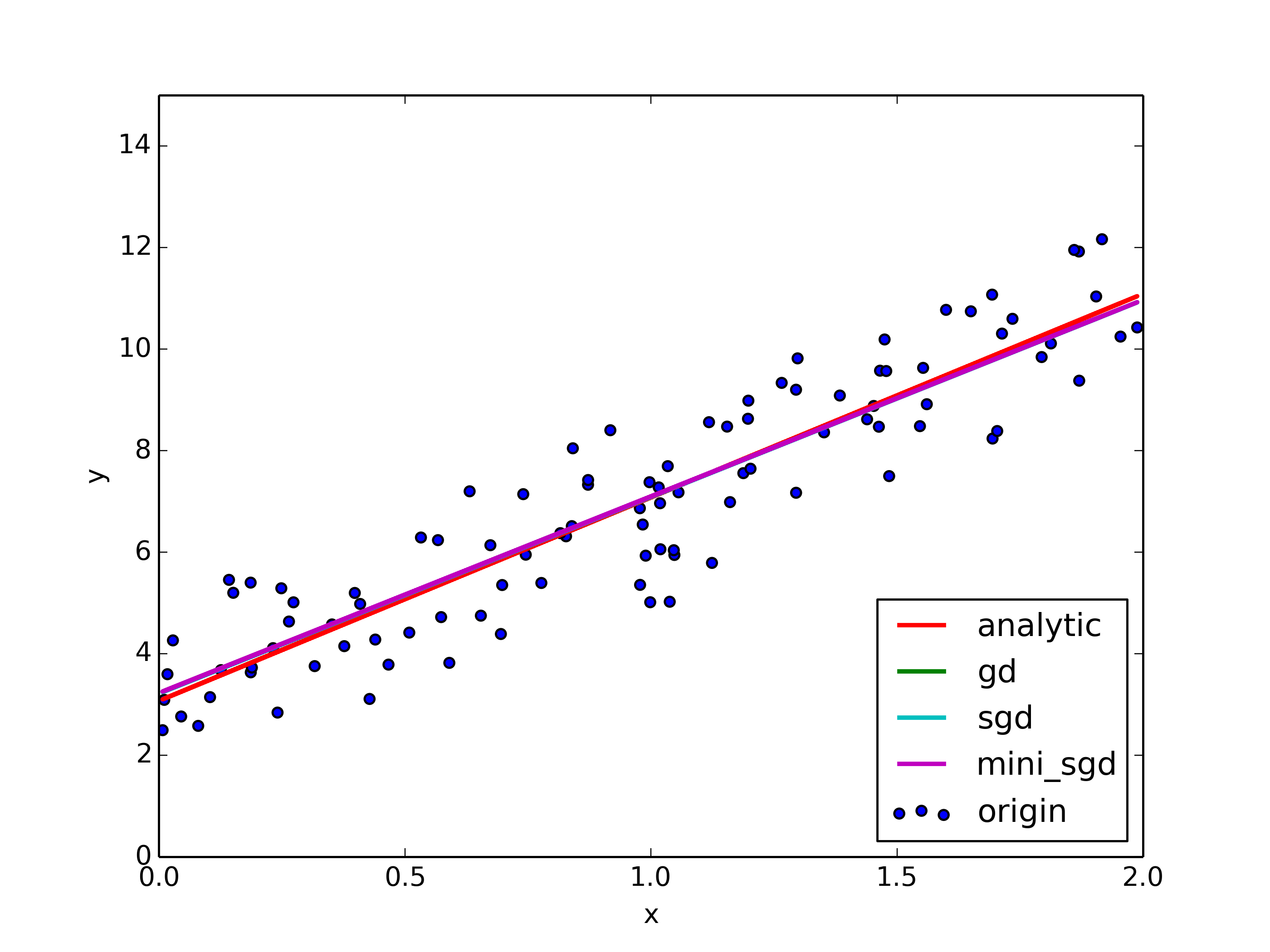
The gradients and the objective convergence

References

Gradient Descent in Python by Sagar Mainkar

You May Also Enjoy