Jiexin Wang

Reinforcement Learning
Mobile & Joint Robots

Definition

Randomness is for exploration

a ~ π(a|s) - policy is defined by a probability distribution, in many RL algorithms

For discrete actions, picking one of many possible actions, a categoritcal distribution is used (left fig)
For continuous actions, a Gaussian with a mean and a std may be used (right fig)

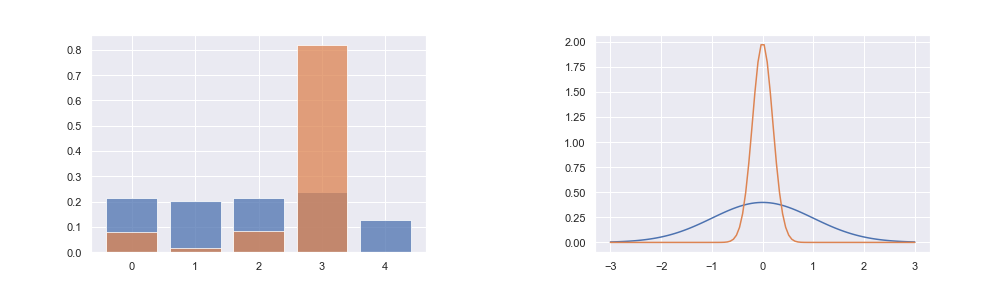
With these kinds of policies, the randomness of the actions an agent takes can be quantified by the entropy of that probability distribution

The greater the entropy, the more random the actions an agent takes
High entropy - more disorer (blue lines in the fig), Low entropy (orange lines in the fig)

Entropy of a discrete probability distribution p:

H(X) = E [I(X)] = - Σ p(x)logp(x)
        X          x∈X

RL process will naturally lead to the entropy of the action selection policy decreasing (from blue lines to oranges lines), i.e. annealing of a Boltzmann softmax policy

Encouraging Entropy
It is also typical to add “entropy bonus” to the loss function to encourage the agent to take actions more unpredictably (with higher randomness)

Entropy Bonus:
(+) avoid an agent quickly converges to a local, but not necessarily globally optimal policy

Similar as optimizing for the long-term sum of future rewards, we can also optimize for the long-term sum of entropy:

It is optimal for an agent to learn not only to get as many future rewards as possible, but also to put itself in positions where its future entropy will be the largest!!

                ∞
π* = argmax E  [Σ γ^t (r+αH^π)]
        π    π t=0     |t |t

High entropy also means adaptive to env changes: keeping pre-existing ways or trying new ways
The key is to plan not only for a good outcome, but the ability to change when the world does!!

High entropy policy:

H(π(.|s)) = - Σ π(a|s)log π(a|s) = E [ -log π(a|s)]
              a                   a~π(.|s)

(+) high entropy policy means higher disorder in policy
(+) try new risky behaviors <=> potentially explore unexplored regions

Standard MDP:

max E [Σ γ^t r(st,at)]
 π   π t

MaxEnt MDP:

max E {Σ γ^t [r(st,at)+H(π(.|st))]}
 π   π t

Theorem 1:
Soft Q-function:

                             ∞
Q^π (st,at) ≜ r(st,at) + E   Σ [γ^l (r(s  , a) + H(π(.|s))]
soft                      π l=1        |t+l |t+l       |t+l

Soft V-function:

V^π (st) ≜ log ∫ exp(Q^π (st,a)) da
soft           A     soft

Optimal value functions:

Q* (st,at) ≜ max Q^π (st,at)
soft          π  soft

V* (st) ≜ log ∫ exp(Q* (st,a)) da
soft                soft

Soft Update Derivation

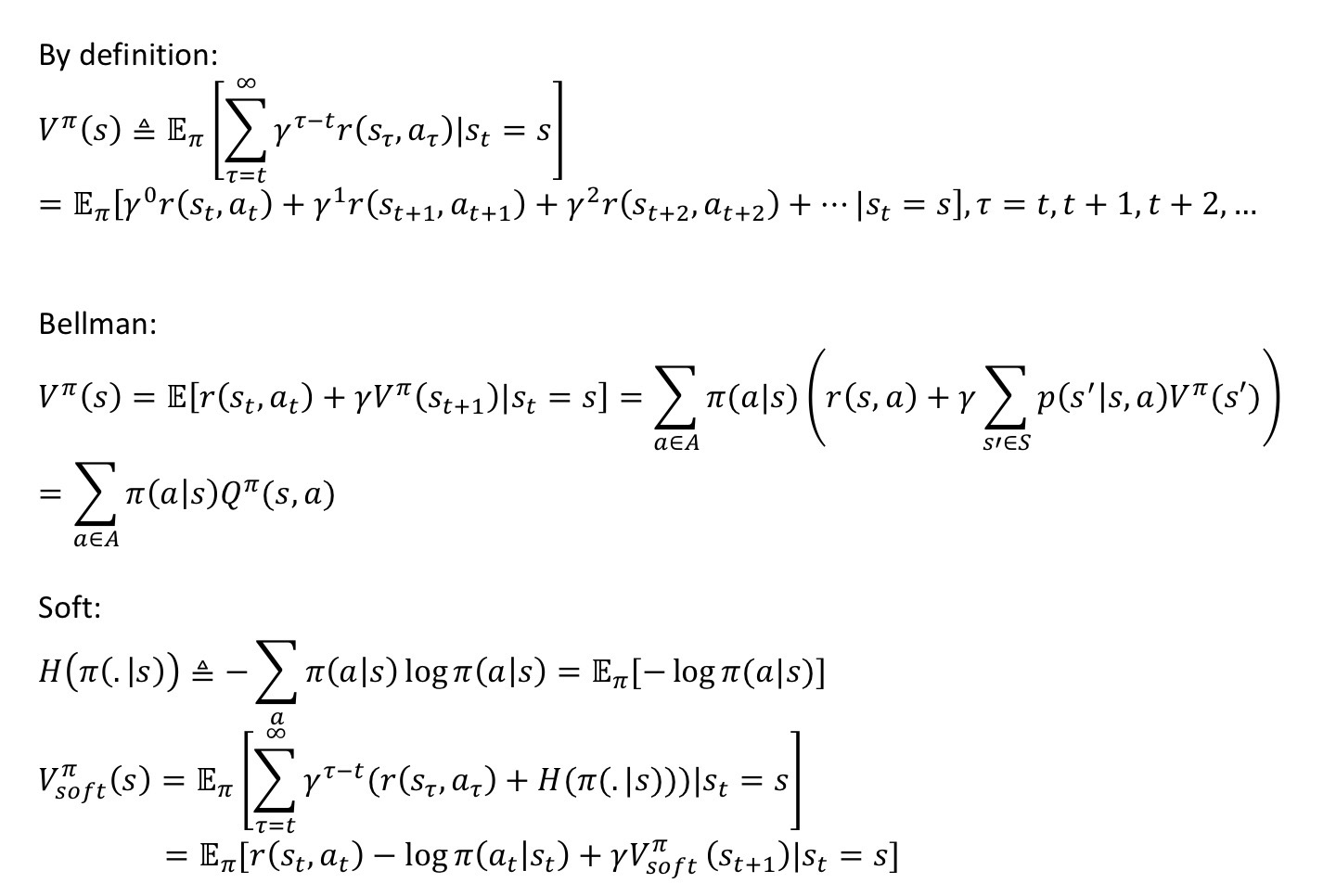
Reference

Maximum Entropy Policies in Reinforcement Learning & Everyday Life
Learning Diverse Skills via Maximum Entropy Deep Reinforcement Learning

https://towardsdatascience.com/in-depth-review-of-soft-actor-critic-91448aba63d4

You May Also Enjoy